组合逻辑设计 ¶
约 2827 个字 预计阅读时间 11 分钟
基本功能块 ¶
译码器 ¶
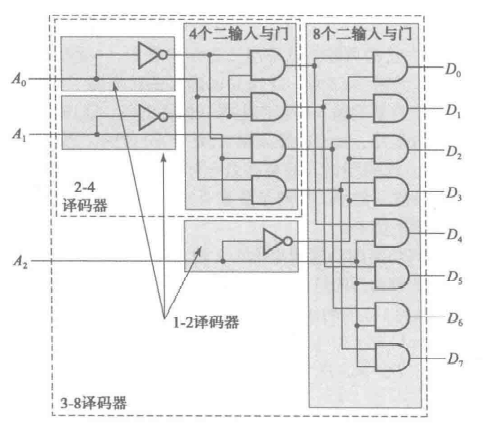
译码器(Decoder)能将信息从 $n$ 个输入转换为 $2^n$ 个或更少的唯一输出。具体是怎么实现的呢?译码器实际上是在枚举 $n$ 个输入的所有排列方式(共 $2^n$ 种101 时,只有相应的表示 101(或者说 $\sum_m(5)$)这个组合的输出是 1。
如何构造一个 $n-to-2^n$ 译码器?我们用递归的思路来求解:
- 设 $k=n$;
- 如果 $k$ 为偶数,问题分解为设计两个 $\frac{k}{2}-to-2^{\frac{k}{2}}$ 译码器,并将它们用 $2^k$ 个与门连接起来;
- 如果 $k$ 为奇数,问题分解为设计一个 $\frac{k-1}{2}-to-2^{\frac{k-1}{2}}$ 和一个 $\frac{k+1}{2}-to-2^{\frac{k+1}{2}}$ 译码器,并将它们用 $2^k$ 个与门连接起来;
- 对每个译码器重复第二步,直到 $k=1$,这时候我们使用一个 $1-to-2$ 译码器;
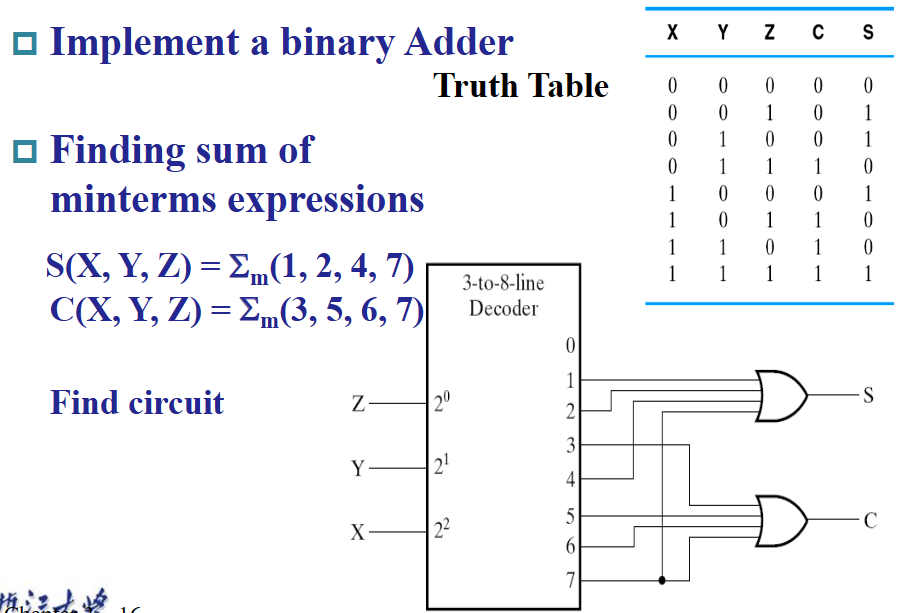
前面提到译码器本质上完成了枚举最小项的工作,如果我们在译码器的输出后面接上或门,就可以实现 SOM 的逻辑表达。因为 SOM 可以表达任何组合逻辑,所以译码器就可以实现任何的组合逻辑。
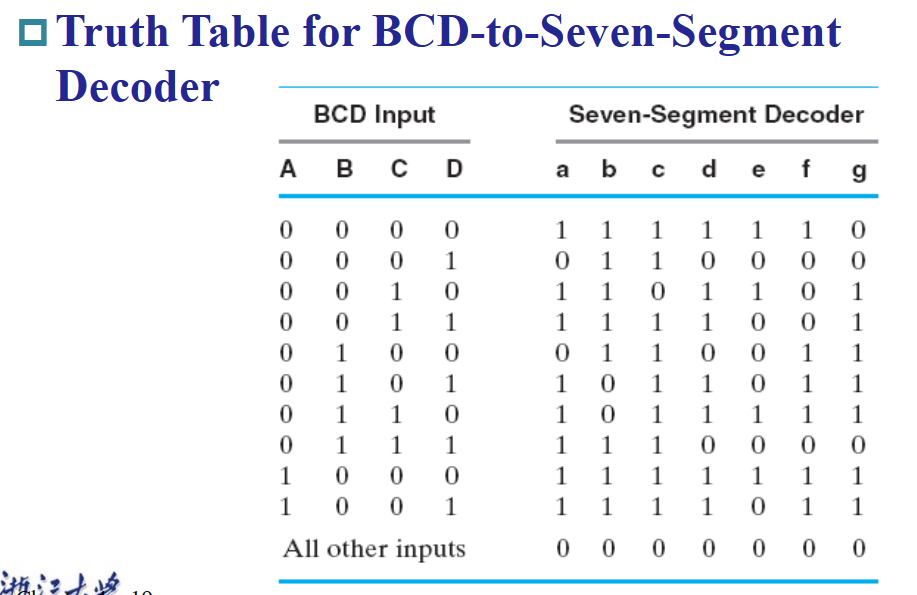
译码器的应用有很多,比如设计加法器、7 段数码管等。
编码器 ¶
编码器(Encoder)与译码器是对称的,能将信息从 $2^n$ 个或更少的输入转换为 $n$ 个输出。但和译码器不同的是,普通编码器必须要求输入是 one-hot 的,即只允许存在一个输入为 1,否则无法判断得出唯一输出。此外,编码器的逻辑表达式和具体电路实现,通常都比译码器更为复杂。
译码器和编码器
译码器和编码器在原理上是对称的,两者的区别在于交换了 $n$ 端和 $2^n$ 端。值得注意的是,$2^n$ 端每次只允许一个信号是活动的(一般来说是 1,其他信号则为 0101 与 $n$ 端的 1 0 1 是唯一对应的。
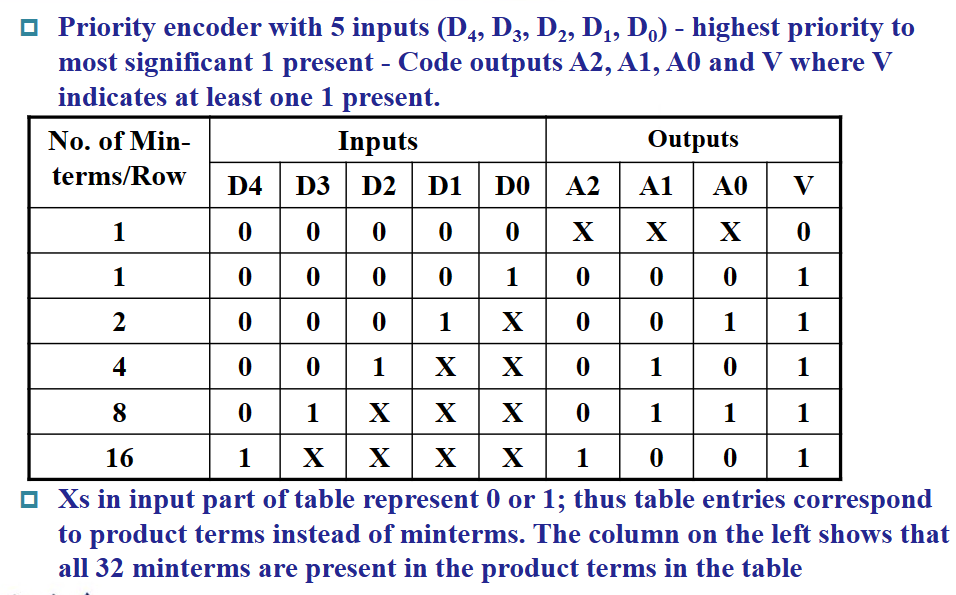
优先编码器(Priority Encoder)可以解决上述问题。在优先编码器中,如果多个输入处在活动状态(输入为 1
多路复用器 ¶
多路复用器(Multiplexer,或称为数据选择器)可以通过 $n$ 个控制信号输入,对 $2^n$ 个或更少的数据信号输入做选择,并得到 $1$ 个选择结果输出。
MUX 和译码器一样,都可以表达任意组合逻辑。这是因为 MUX 的实现内部就存在一个译码器,我们只需要将 MUX 的控制端(也就是译码器)用作输入,将组合逻辑的真值表写入 MUX 的选项端进行选择,就可以表达任何组合逻辑。
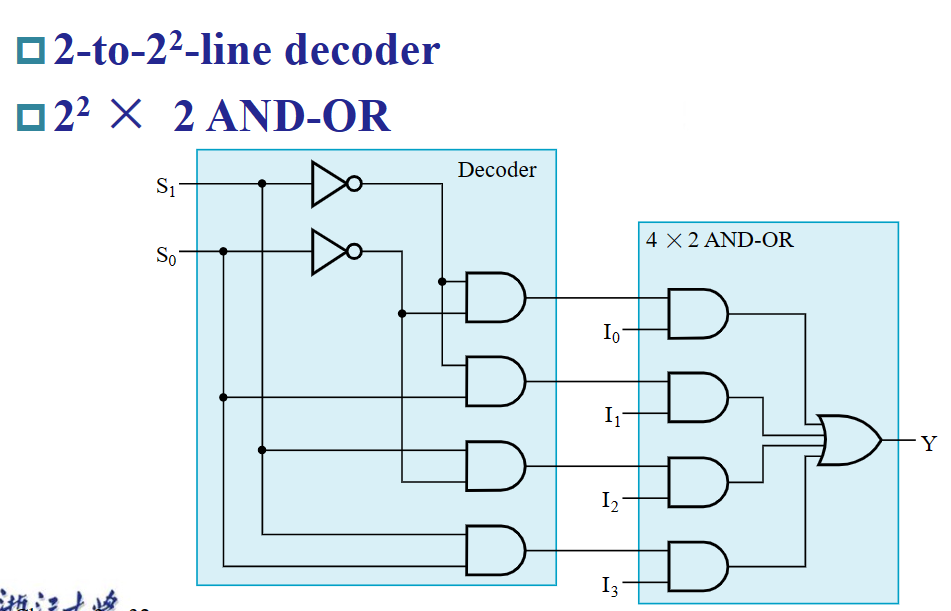
通常,一个 $2^n-to-1$ MUX 的组成为:
- 一个 $n-to-2^n$ 译码器(MUX 利用了译码器每次只有一个输出为
1的特性,从而实现选择功能) ; - $2^n \times 2$ AND-OR;
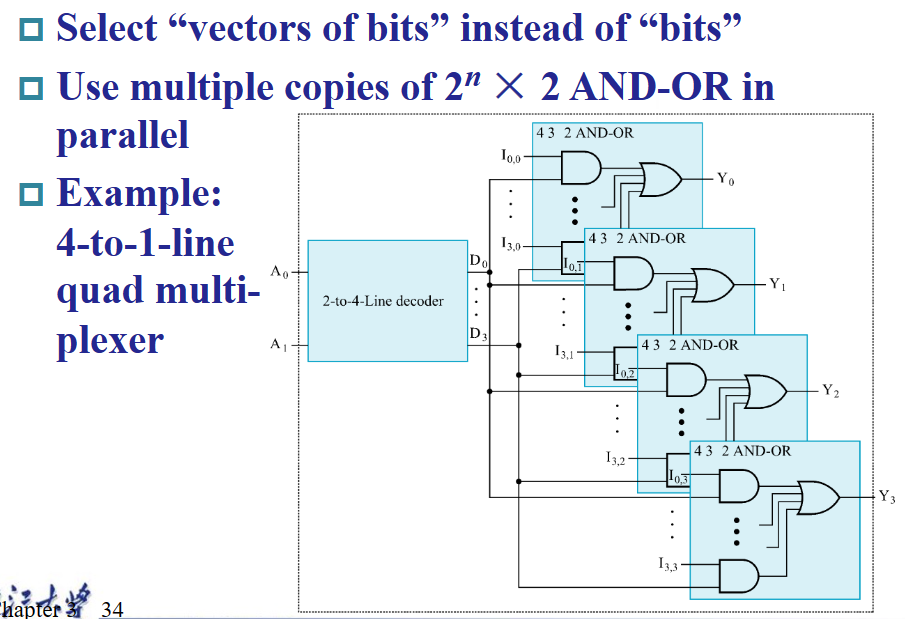
当然,多路复用器不止可以选择单个数据信号,也可以选择一组数据信号(或称向量形式的数据信号
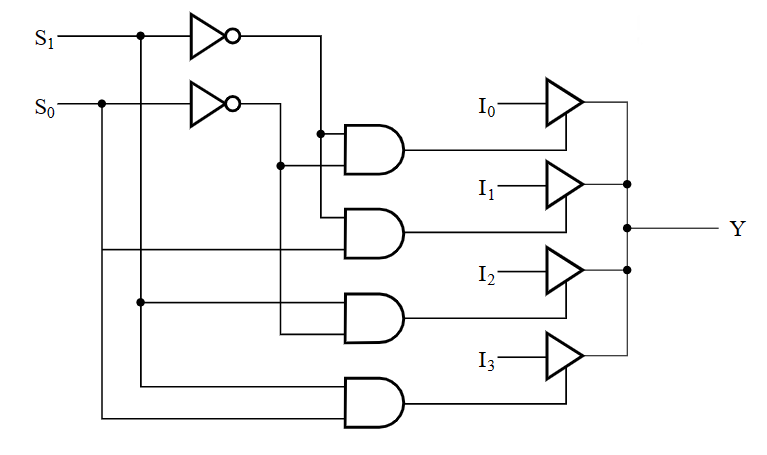
除了多路复用器,选择器还有其他的电路实现方法,比如三态门和传输门。
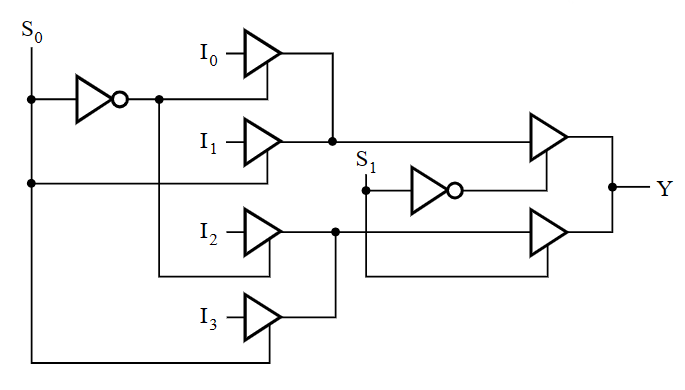
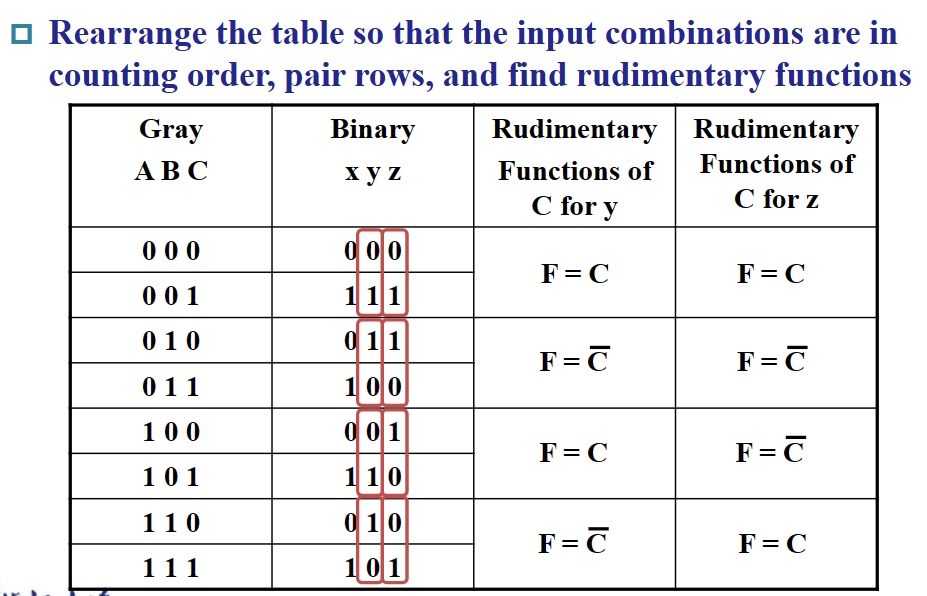
MUX 的电路实现有一种优化方案,就是通过把一部分的控制端的输入写到选项端作为常量来被选择,从而简化元件(降维
MUX 的降维优化
注:上图有误,应该是 $4-to-1$ MUX。
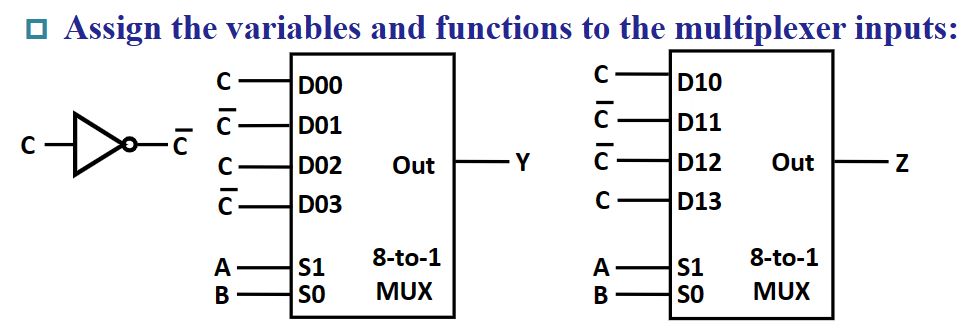
我们可以通过组合逻辑表达式来更深刻地理解为什么可以这样做(以 $Y$ 举例
$$ \begin{aligned} Y & = \overline{A}\overline{B}C+\overline{A}B\overline{C}+A\overline{B}C+AB\overline{C} \cr & = \overline{A}\overline{B}\overline{C}\cdot 0+\overline{A}\overline{B}C\cdot 1+\overline{A}B\overline{C}\cdot 1+\overline{A}BC\cdot 0+A\overline{B}\overline{C}\cdot 0+A\overline{B}C\cdot 1+AB\overline{C}\cdot 1+ABC\cdot 0 \cr & = \overline{A}\overline{B}(\overline{C}\cdot 0+C\cdot 1)+\overline{A}B(\overline{C}\cdot 1+C\cdot 0)+A\overline{B}(\overline{C}\cdot 0+C\cdot 1)+AB(\overline{C}\cdot 1+C\cdot 0) \end{aligned} $$
译码器与多路复用器
译码器和多路复用器的原理与实现都有相似之处。如果我们要实现任何组合逻辑,大部分情况下使用译码器会更好,因为它只需要把枚举出的最小项用一个或门连接即可,而 MUX 则需要用很多的与门来达到相同的效果。当然,在某些情况下 MUX 可以进行降维优化,有时候会比译码器效果更好。
事实上,这样的比较不算公平,因为它们虽然很相似,但设计的目的是差别很大的。译码器用于译码(interpret a coded data
算术逻辑电路 ¶
从全加器到超前进位加法器 ¶
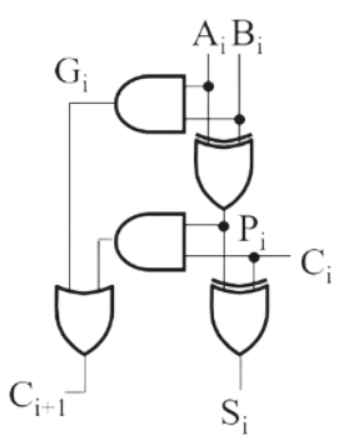
首先我们先把注意力放在一个全加器上。要把多个全加器连接起来形成能够计算更大数据的加法器,关键在于如何处理好全加器之间「进位」的问题。对于一个全加器而言,它向后一个全加器的进位($C$,carry)有两个来源,一个是自身加法产生的进位,记为 $G$(generate
$$ C_{i+1} = A_i B_i + (A_i \oplus B_i) C_i = G_i + P_i \cdot C_i $$
具体电路实现如下图:
最自然的想法是把全加器直接链式连接,即直接把前一个全加器的进位连接到后一个全加器上,这样的做法叫做行波加法器(ripple-carry adder
所以,有没有办法提前把进位传递下去,而不需要等待前面的全加器完全计算完毕呢?超前进位加法器(carry-lookahead adder, or CLA)就是用来解决这个问题的。那么超前进位加法器是怎么做到提前把进位传递下去的呢?让我们再把注意力转向公式推导:
$$ C_1 = G_0 + P_0 C_0 $$
$$ \begin{aligned} C_2 & = G_1 + P_1 C_1 = G_1 + P_1 (G_0 + P_0 C_0) \cr & = G_1 + P_1 G_0 + P_1 P_0 C_0 \end{aligned} $$
$$ \cdots $$
$$ C_4 = G_3 + P_3 G_2 + P_3 P_2 G_1 + P_3 P_2 P_1 G_0 + P_3 P_2 P_1 P_0 C_0 $$
我们发现,$C_4$ 不再依赖于 $C_3$,而是直接依赖于 $C_0$。我们只需要并行计算每个全加器的 $P$ 和 $G$,然后把 $C_0$ 与它们结合即可计算得出每个全加器向后传递的进位 $C_{i+1} = G_{0\sim i} + P_{0\sim i} C_0$。
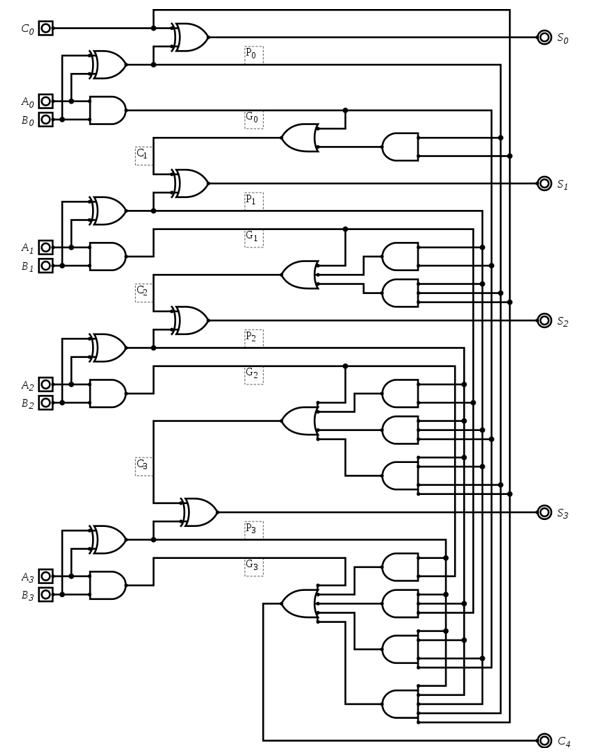
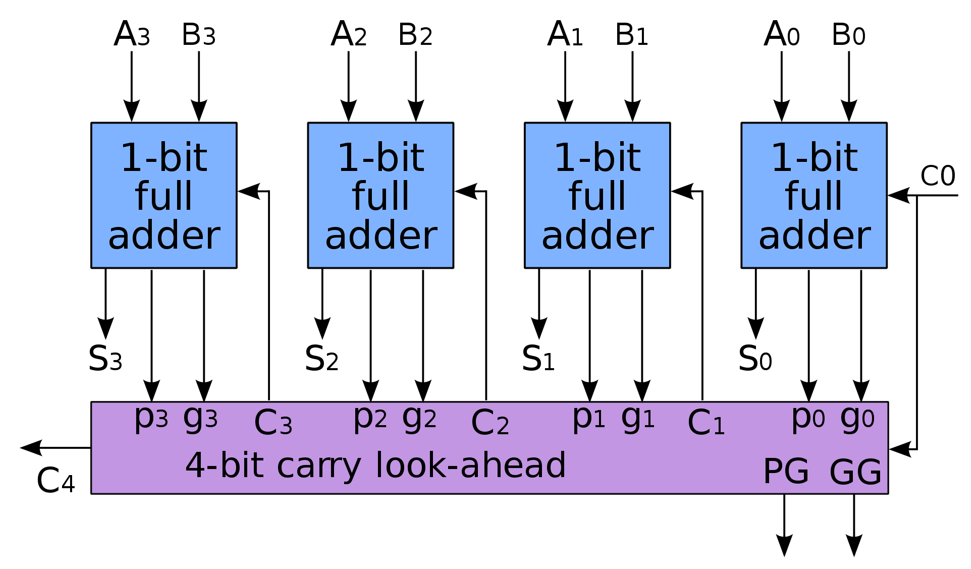
具体电路实现如下图,我们发现所有全加器的 $P$ 和 $G$ 都是并行计算的,而对于每个进位的计算,只需要额外消耗 $C_0$ 经过一个与门和一个或门的时间:
但我们发现,这样的超前进位加法器虽然解决了进位延迟的问题,但是仍然无法大规模使用,问题的关键在于电路中的多输入与门和或门,如果我们要连接 $n$ 个全加器,那么就需要 $n+1$ 输入的与门和或门,这是不现实的。所以我们考虑把这一个 4-bit 超前进位加法器作为一个模块,并在此基础上组建更大的超前进位加法器。
$$ C_4 = G_{0\sim 3} + P_{0\sim 3} C_0 $$
$$ C_8 = G_{4\sim 7} + P_{4\sim 7} C_4 $$
$$ \cdots $$
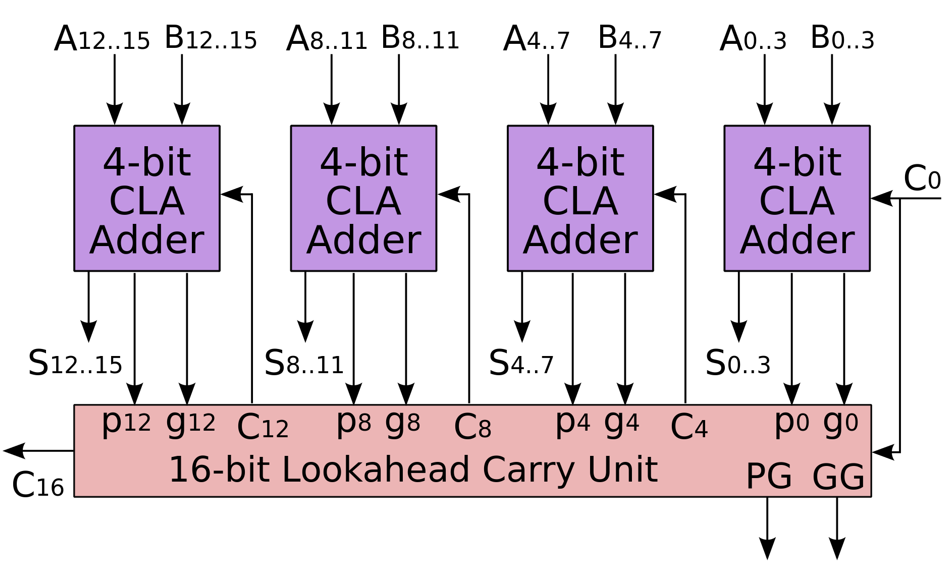
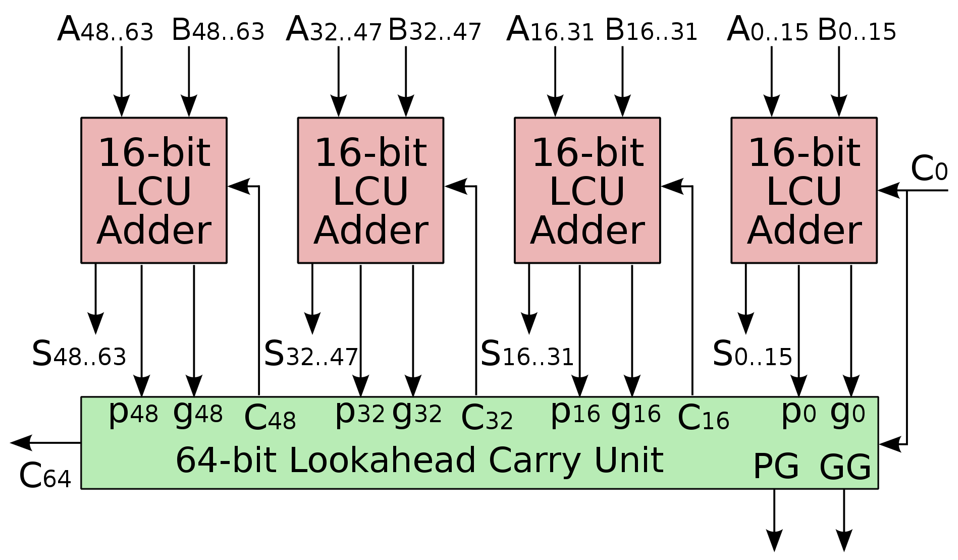
$$ \begin{aligned} C_{16} & = G_{12\sim 15} + P_{12\sim 15} C_12 \cr & = G_{12\sim 15} + P_{12\sim 15} G_{8\sim 11} + P_{12\sim 15} P_{8\sim 11} G_{4\sim 7} \cr & + P_{12\sim 15} P_{8\sim 11} P_{4\sim 7} G_{0\sim 3} + P_{12\sim 15} P_{8\sim 11} P_{4\sim 7} P_{0\sim 3} C_0 \end{aligned} $$
我们惊讶地发现,这个 $C_{16}$ 表达式的写法和之前推导超前进位加法器时 $C_4$ 的写法是完全一致的,只需要做一些下标变换即可。这就启发我们如何组建更大规模的超前进位加法器:我们把若干个小的超前进位加法器连接起来,就像我们当初把若干个全加器连接成超前进位加法器一样!
加减法的溢出检查 ¶
常见的加减法溢出情况是,同号相加和异号相减。下面给出两种最简单的溢出检查(overflow detection
- 检查输出的符号位和加数或减数(top operand)的符号位是否一致
- 对于 $n$ 位加减法,溢出可以表示为 $V=C_n\oplus C_{n-1}$,$V$ 为
1表示溢出
其他算数函数 ¶
- 自增(incrementing)与自减(decrementing)
- 自增与自减运算可以通过对加减法器进行收缩(contraction)得到
- 具体而言就是把加减法器的其中一个输入设为常量(自增自减的步长)
- 乘法与除法
- 与 $2^n$ 的乘数是最简单的,只需要通过移位就可以实现
- 任意常数的乘除的一种实现思路是,拆分成与若干个 $2^n$ 的乘除
- 零扩展(zero fill)与符号位扩展(extension)
创建日期: 2024年2月8日 16:17:32