量子基础 ¶

信息、熵与计算复杂度 ¶

香农熵 ¶

消息的信息量取决于消息内容令人惊讶的程度，被定义为一个随着事件发生概率 $p$ 减小而增大的函数 $I(p)$。

可以这样去理解信息量与概率的关系：知道某个特定数字不会成为彩票中奖号码所提供的信息量非常少，因为任何选定的数字几乎都不会中奖；但是知道某个特定数字会中奖所提供的信息量则是巨大的，因为它传递了极低概率事件的结果。

信息量函数 $I(p)$ 满足如下性质：

• 连续性：$I(p)$ 是关于 $p$ 的连续函数
• 可加性：$I(p_x, p_y) = I(p_x) + I(p_y)$ 对于独立事件 $x, y$ 均成立

根据这两条性质可以推导出：

• 由可加性，对于任意实数 $r$，有 $I(p_x ^ r) = rI(p_x)$
• 进一步地，由连续性，有 $I(p_x) = I((½) ^ {-\log _2 (p_x)}) = -\log _2 (p_x) I(½)$

常数 $I(½)$ 可以被视作信息量的单位，从而可以定义香农熵：

• 发生概率为 $p_x$ 的事件 $x$ 的香农熵为 $-\log _2 (p_x)$
• 一系列发生概率分别为 $p_1, p_2, ..., p_n$ 的事件的平均信息量为 $H \sim -\sum _{i=1} ^ n p_i \log _2 p_i$

香农熵的一个重要应用是香农源编码理论：对于源为独立同分布随机变量的数据，香农熵提供了一个数据压缩的下界。具体而言，当数据量趋于无穷时，不可能压缩这些数据以使得码率（每个符号的平均 bit 位数）小于源的香农熵 $H$。

计算复杂度 ¶

• P：代表所有可在多项式时间内解决的决策问题，这类问题往往是易于解决的
• NP：代表所有可在多项式时间内验证的决策问题，即对于任一给定的猜测，都可以在多项式时间内判断猜测是否正确
  • 显然 P $\sube$ NP，而著名的 P = NP? 问题至今未被解决
  • NP 完全问题是 NP 中最难的一些问题，在多项式时间内解决此类问题的算法也能在多项式时间内解决任何其他 NP 问题
• BPP：如果存在满足以下性质的算法，则决策问题属于 BPP
  • 允许抛硬币并做出随机决定；保证在多项式时间内运行；对于算法的任何一次运行，给出错误答案的概率不超过 ⅓
  • 显然 P $\sube$ BPP，随着越来越多 BPP 问题被证明属于 P，人们推测 P = BPP（去随机化）
• BQP：代表所有可由量子计算机在多项式时间内以高概率解决的决策问题，可以视作 BPP 问题的量子推广
  • 有 BPP $\sube$ BQP，而 BPP = BQP? 是未知的

复向量空间下的光子及其量子态 ¶

狄拉克记号 ¶

狄拉克记号广泛应用于量子信息领域，其基本记法如下：

• 复向量空间 $V$ 中的向量记为 $\ket{v}$，线性泛函 $f: V \rightarrow \Complex$ 记为 $\bra{f}$，线性泛函作用于向量记为 $\braket{f|v} \in \Complex$
• 复向量内积空间 $V$ 中有内积 $(\cdot , \cdot)$ 且第一位是共轭线性的，对于向量 $\phi$ 可以定义 $(\phi , \cdot) \equiv \bra{\phi}$，其中线性泛函 $\bra{\phi}$ 是向量 $\ket{\phi}$ 的伴随（矩阵形式的共轭转置），从而内积记为 $(\phi , \psi) \equiv \braket{\phi | \psi}$
  • 内积 $\braket{\phi | \psi}$ 表示 $\ket{\psi}$ 投影到 $\ket{\phi}$ 上，注意 $\braket{\phi | \psi} = \braket{\psi | \phi} ^ *$
• 线性泛函 $\bra{\phi}$ 和向量 $\ket{\psi}$ 可以通过外积结合成算子 $\ket{\psi} \bra{\phi}$，定义为 $\ket{\psi} \bra{\phi} : \ket{\xi} \mapsto \ket{\psi} \braket{\phi | \xi}$
  • 外积 $P_k \equiv \ket{k} \bra{k}$ 表示 $\ket{k}$ 方向的投影算子，$P_k \ket{v} = \ket{k} \braket{k | v}$

从矩阵形式思考，狄拉克记号下线性泛函与向量的结合遵循矩阵乘法：

• $\braket{\phi | \psi} \doteq \begin{pmatrix} \phi _1 ^ * & \phi _2 ^ * & \cdots & \phi _N ^ * \end{pmatrix} \begin{pmatrix} \psi _1 \cr \psi _2 \cr \vdots \cr \psi _N \end{pmatrix} = \sum _ {i=1} ^ N \phi _i ^ * \psi _i$
• $\ket{\phi} \bra{\psi} \doteq \begin{pmatrix} \phi _1 \cr \phi _2 \cr \vdots \cr \phi _N \end{pmatrix} \begin{pmatrix} \psi _1 ^ * & \psi _2 ^ * & \cdots & \psi _N ^ * \end{pmatrix} = \begin{pmatrix} \phi _1 \psi _1 ^ * & \phi _1 \psi _2 ^ * & \cdots & \phi _1 \psi _N ^ * \cr \phi _2 \psi _1 ^ * & \phi _2 \psi _2 ^ * & \cdots & \phi _2 \psi _N ^ * \cr \vdots & \vdots & \ddots & \vdots \cr \phi _N \psi _1 ^ * & \phi _N \psi _2 ^ * & \cdots & \phi _N \psi _N ^ * \end{pmatrix}$

光的偏振 ¶

光的偏振是二维复向量空间的一个范例，或者说光的偏振是量子比特 qubit 的一个范例，可以用一个二维复向量来表示一个偏振光。

• 线偏振光：$\begin{cases} E_x = E_0 \cos \theta \cos \omega t \cr E_y = E_0 \sin \theta \cos \omega t \end{cases}$
  • 可以用单位复向量 $\ket{p} = (\cos \theta , \sin \theta) ^ T$ 表示这个线偏振光
  • Malus 定律 $I ^ {\prime} = I \cos ^ 2 \theta$ 的统计学描述：偏振方向为 $\ket{p} = (\cos \theta , \sin \theta) ^ T$ 的 $N$ 个光子透过偏振方向为 $\ket{n} = (1, 0) ^ T$ 的偏振片，透过率约为 $N_x / N \simeq \cos ^ 2 \theta = \braket{p | n}$
• 椭圆偏振光：$\begin{cases} E_x = E_0 \cos \theta \cos (\omega t - \delta _x) = E_0 \text{Re} (\mu e ^ {-i\omega t}) & ,\; \mu = \cos \theta e ^ {i\delta _x} \cr E_y = E_0 \sin \theta \cos (\omega t - \delta _y) = E_0 \text{Re} (\nu e ^ {-i\omega t}) & ,\; \nu = \sin \theta e ^ {i\delta _y} \end{cases}$
  • 可以用单位复向量 $\ket{p} = (\mu, \nu) ^ T$ 表示这个椭圆偏振光，由于物理上相位差 $\delta = \delta _y - \delta _x$ 才是有意义的，因此 $\ket{p}$ 可由两个实参数 $\theta , \delta$ 唯一确定
  • 圆偏振光的 $\theta = \pi / 4$ 且 $\delta = \pm \pi / 2$，可以用单位复向量 $\frac{1}{\sqrt{2}} (1 , \pm i) ^ T$ 表示

下面考虑用狄拉克记号表达光的偏振（以线偏振光为例）：

• 引入正交基 $\ket{h} = \begin{pmatrix} 1 \cr 0 \end{pmatrix} , \ket{v} = \begin{pmatrix} 0 \cr 1 \end{pmatrix}$，以及相应的投影算子 $P_h = \ket{h} \bra{h} = \begin{pmatrix} 1 & 0 \cr 0 & 0 \end{pmatrix} , P_v = \ket{v} \bra{v} = \begin{pmatrix} 0 & 0 \cr 0 & 1 \end{pmatrix}$，注意到 $P_h + P_v = I _ {2\times 2}$
• 从而线偏振光可以表示为 $\ket{p} = I _ {2\times 2} \ket{p} = \ket{h} \bra{h} \ket{p} + \ket{v} \bra{v} \ket{p} = \mu \ket{h} + \nu \ket{v}$，注意到 $|\mu| ^ 2 + |\nu| ^ 2 = 1$
  • $\mu = \braket{h | p} , \nu = \braket{v | p}$ 称为概率幅，分别反映了量子态 $\ket{p}$ 坍缩到 $\ket{h}$ 和 $\ket{v}$ 的可能性
  • 概率幅的模平方表示概率，例如 $\text{P} _ h = |\mu| ^ 2 = \braket{p | h} \braket{h | p} \equiv \braket{p | P _ h | p}$，其中 $\text{P}_h$ 表示概率而 $P_h$ 表示 $\ket{h}$ 对应的投影算子

自旋、量子比特与线性算子 ¶

自旋与线性算子 ¶

孤立的 ½ 自旋是量子比特 qubit 的一个范例，可以用一个二维复向量来表示一个 ½ 自旋状态。

• 引入正交基 $\ket{0} \equiv \ket{\uparrow} = \begin{pmatrix} 1 \cr 0 \end{pmatrix} , \ket{1} \equiv \ket{\downarrow} = \begin{pmatrix} 0 \cr 1 \end{pmatrix}$
• 任意自旋状态都可以表示为 $\ket{\uparrow}$ 和 $\ket{\downarrow}$ 这两种自旋状态的叠加 $\ket{\psi} = \alpha \ket{\uparrow} + \beta \ket{\downarrow}$ 且 $|\alpha| ^ 2 + |\beta| ^ 2 = 1$

对系统的自旋状态的观测用一个厄米的（Hermitian）线性算子表示。

• 考虑其特征方程 $M \ket{\lambda} = \lambda \ket{\lambda}$，每个特征值 $\lambda$ 都是实的
• 考虑其特征分解 $M = \sum _ {\lambda \lambda ^ \prime} \ket{\lambda} \bra{\lambda} M \ket{\lambda ^ \prime} \bra{\lambda ^ \prime} = \sum _ {\lambda} \lambda \ket{\lambda} \bra{\lambda} = \sum _{\lambda} \lambda P _ {\lambda}$
• 对于自旋状态 $\ket{\psi}$ 和观测 $M$，观测到特征向量 $\ket{\lambda}$ 表示的自旋状态的概率为 $\text{P} _ {\lambda} = \braket{\psi | \lambda} \braket{\lambda | \psi}$
• 对于自旋状态 $\ket{\psi}$ 和观测 $M$，定义期望为 $\braket{M} \equiv \braket{\psi | M | \psi} = \sum _ {\lambda} \lambda \braket{\psi | \lambda} \braket{\lambda | \psi} = \sum _ {\lambda} \lambda \text{P} _ {\lambda}$
• 观测是不可逆的，经过观测的系统会坍缩到其一特征向量表示的自旋状态（经典的 Stern-Gerlach 实验反映了观测如何影响 ½ 系统的自旋状态）；我们无法预测系统会坍缩到哪种状态，但我们能分析系统坍缩到这些状态的概率

泡利矩阵 ¶

泡利矩阵是三个厄米的 $2 \times 2$ 复向量矩阵，它们本身即可表示三种观测；更为重要的是，它们的线性组合可以构造出沿着任意自旋方向的观测。

三个泡利矩阵及其特征向量如下（注意它们的特征值都是 $\pm 1$，分别对应两种正交的自旋状态）：

• $\sigma _ z = \begin{pmatrix} 1 & 0 \cr 0 & -1 \end{pmatrix}$，对应 $\ket{0}$ 和 $\ket{1}$
• $\sigma _ x = \begin{pmatrix} 0 & 1 \cr 1 & 0 \end{pmatrix} \;\;$，对应 $\ket{r} = \frac{1}{\sqrt{2}} \ket{0} + \frac{1}{\sqrt{2}} \ket{1}$ 和 $\ket{l} = \frac{1}{\sqrt{2}} \ket{0} - \frac{1}{\sqrt{2}} \ket{1}$
• $\sigma _ y = \begin{pmatrix} 0 & -i \cr i & 0 \end{pmatrix}$，对应 $\ket{i} = \frac{1}{\sqrt{2}} \ket{0} + \frac{i}{\sqrt{2}} \ket{1}$ 和 $\ket{o} = \frac{1}{\sqrt{2}} \ket{0} - \frac{i}{\sqrt{2}} \ket{1}$

下面展示如何通过泡利矩阵构造出沿着任意自旋方向的观测矩阵：

• 在现实中，自旋方向是由一个三维实向量表示的；而在量子力学中，自旋状态是由一个二维复向量表示的
• 定义泡利向量 $\vec{\sigma} = \sigma _ x \hat{x} + \sigma _ y \hat{y} + \sigma _ z \hat{z}$，对于自旋方向 $\hat{n} = (n_x, n_y, n_z)$，沿着这个方向的观测可以表示成矩阵 $\sigma _ n = \vec{\sigma} \cdot \hat{n} = \sigma _ x n _ x + \sigma _ y n _ y + \sigma _ z n _ z = \begin{pmatrix} n _ z & n _ x - i n _ y \cr n _ x + i n _ y & - n _ z \end{pmatrix}$，注意到这个矩阵的特征值也为 $\pm 1$，分别对应沿着这个自旋方向的两种正交的自旋状态
• 借助泡利向量，我们可以根据任意由三维实向量表示的自旋方向来构造相应的由二维复厄米矩阵表示的观测

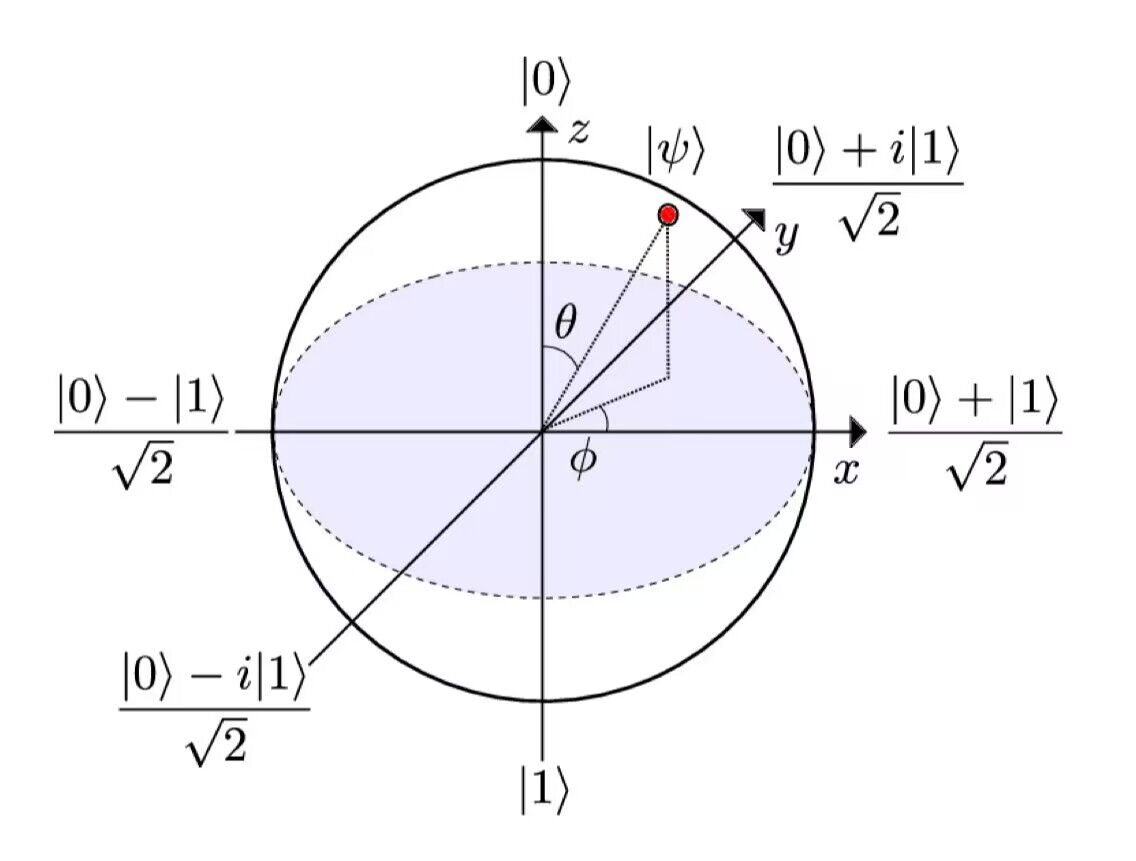
Bloch 球 ¶

Bloch 球是 qubit 的一种几何表示：

• Bloch 球表面上每一个点都表示一种量子状态（自旋状态）
• Bloch 球中每条穿过球心的轴的两极都表示一对正交的量子状态
• Bloch 球的 $x,y,z$ 轴分别表示三个泡利矩阵对应的正交量子状态
• 量子状态记为 $\ket{\psi} = \cos (\theta / 2) \ket{0} + e ^ {i \phi} \sin (\theta / 2) \ket{1}$

关于“为什么 Bloch 球要这样定义”，下面给出一种解释：

首先取基状态 $\ket{0}$ 和 $\ket{1}$，任意量子状态可以表示为基状态的叠加 $\ket{\psi} = \alpha \ket{0} + \beta \ket{1}$，其中 $|\alpha| ^ 2 + |\beta| ^ 2 = 1$；然后考虑以这个量子状态及其正交态 $\ket{\bar{\psi}} = \beta ^ * \ket{0} - \alpha ^ * \ket{1}$ 作为特征向量，利用特征分解构造一个观测：

$$ M = \sum _ {\lambda = \pm 1} \lambda P _ \lambda = \ket{\psi} \bra{\psi} - \ket{\bar{\psi}} \bra{\bar{\psi}} = \begin{pmatrix} |\alpha| ^ 2 - |\beta| ^ 2 & 2\alpha \beta ^ * \cr 2\alpha ^ * \beta & |\beta| ^ 2 - |\alpha| ^ 2 \end{pmatrix} $$

注意到沿着自旋方向 $\hat{n} = (n_x, n_y, n_z)$ 构造的观测可以表示成矩阵 $\sigma _ n = \vec{\sigma} \cdot \hat{n} = \sigma _ x n _ x + \sigma _ y n _ y + \sigma _ z n _ z = \begin{pmatrix} n _ z & n _ x - i n _ y \cr n _ x + i n _ y & - n _ z \end{pmatrix}$；从而我们可以找到观测 $M$ 对应的自旋方向 $\hat{\psi} = (\psi _ x, \psi _ y, \psi _ z)$，其中 $\psi _ z = |\alpha| ^ 2 - |\beta| ^ 2 ,\; \psi _ x + i\psi _ y = 2\alpha ^ * \beta$。

这时候如果我们取 $\alpha = \cos (\theta / 2) ,\; \beta = \sin (\theta / 2) e ^ {i\phi}$（正如 Bloch 球定义的那样），观测对应的自旋方向可以记为 $\hat{\psi} = (\sin {\theta} \cos {\phi} , \sin {\theta} \sin {\phi} , \cos {\theta})$；注意到这时候自旋方向具有了极坐标的形式，也就是说，Bloch 球一方面可视化了由二维复向量表示的 qubit，另一方面可视化了由三维实向量表示的自旋方向，而且这两者在 Bloch 球中是完全重合的。

值得强调的是，上文描述的 Bloch 球中同一点对应的量子状态与自旋方向是有实际联系的。对于量子态 $\ket{\psi} = \cos (\theta / 2) \ket{0} + e ^ {i \phi} \sin (\theta / 2) \ket{1}$，总能找到一个特定方向 $\hat{n}$，使得相应的观测期望为 $\braket{\vec{\sigma} \cdot \hat{n}} = 1$，而这个方向恰为 $\hat{n} = (\sin {\theta} \cos {\phi} , \sin {\theta} \sin {\phi} , \cos {\theta})$。

多量子比特与量子纠缠 ¶

多量子比特系统 ¶

由多个量子比特组成的系统可以分为直积态和纠缠态，这里以 two-qubit 系统为例。首先定义张量积如下：

$$ A \otimes B = \begin{pmatrix} a _ {11} B & a _ {12} B & \cdots & a _ {1n} B \cr a _ {21} B & a _ {22} B & \cdots & a _ {2n} B \cr \vdots & \vdots & \ddots & \vdots \cr a _ {n1} B & a _ {n2} B & \cdots & a _ {nn} B \end{pmatrix} $$

取任意两个 qubit 分别为 $\alpha _ 1 \ket{0} + \beta _ 1 \ket{1}$ 和 $\alpha _ 2 \ket{0} + \beta _ 2 \ket{1}$，使用张量积构建直积态的 two-qubit 系统：

$$ (\alpha _ 1 \ket{0} + \beta _ 1 \ket{1}) \otimes (\alpha _ 2 \ket{0} + \beta _ 2 \ket{1}) = \alpha _ 1 \alpha _ 2 \ket{00} + \alpha _ 1 \beta _ 2 \ket{01} + \beta _ 1 \alpha _ 2 \ket{10} + \beta _ 1 \beta _ 2 \ket{11} $$

对于直积态的 two-qubit 而言，这两个 qubit 是独立的、可分的，可以仅对其中一个 qubit 进行操作：

$$ (L \otimes I) (\ket{u} \otimes \ket{v}) = (L \ket{u}) \otimes \ket{v} $$

不同于直积态，纠缠态的 two-qubit 不能拆分成张量积的形式，两个 qubit 是相互纠缠、非独立的。

例如贝尔态（纠缠态的一个范例），取 $\ket{\Psi _ {+}} = \frac{1}{\sqrt{2}} (\ket{01} + \ket{10})$，注意到如果第一个 qubit 处于状态 $\ket{0}$，则第二个 qubit 必然处于状态 $\ket{1}$，反之亦然。

贝尔态 ¶

贝尔态具有四个基状态：

• $\ket{\Phi _ {+}} = \frac{1}{\sqrt{2}} (\ket{00} + \ket{11})$，$\ket{\Phi _ {-}} = \frac{1}{\sqrt{2}} (\ket{00} - \ket{11})$
• $\ket{\Psi _ {+}} = \frac{1}{\sqrt{2}} (\ket{01} + \ket{10})$，$\ket{\Psi _ {-}} = \frac{1}{\sqrt{2}} (\ket{01} - \ket{10})$

为了进一步理解直积态和纠缠态的区别，我们考虑仅对第一个 qubit 进行观测：

• 对于直积态，两个 qubit 是完全独立的，因此仅对第一个 qubit 进行观测的结果与直接对单个 qubit 进行观测是一样的
  • 取 $\ket{\psi} = \cos (\theta / 2) \ket{0} + e ^ {i \phi} \sin (\theta / 2) \ket{1}$，总能找到一个特定方向 $\hat{n} = (\sin {\theta} \cos {\phi} , \sin {\theta} \sin {\phi} , \cos {\theta})$，使得相应的观测期望为 $\braket{\vec{\sigma} \cdot \hat{n}} = 1$
• 对于纠缠态，两个 qubit 是相互纠缠的，而且仅对第一个 qubit 进行观测是无法得到有效信息的
  • 取贝尔基 $\ket{\Psi _ {+}}$，对任意方向 $\hat{n}$，均有 $\braket{\vec{\sigma ^ {(1)}} \cdot \hat{n}} = 0$，其中观测严格来说应该写为 $(\vec{\sigma ^ {(1)}} \cdot \hat{n}) \otimes I$；即仅对第一个 qubit 进行的任何观测期望均为 0，观测结果等可能地分布于 $\pm 1$，无法得到任何信息

如果想要得到非零的观测结果（即包含有效信息的观测结果），需要对纠缠态整体进行观测，例如：

$$ \sigma ^ {(1)} \cdot \sigma ^ {(2)} = \sigma ^ {(1)} _ {x} \sigma ^ {(2)} _ {x} + \sigma ^ {(1)} _ {y} \sigma ^ {(2)} _ {y} + \sigma ^ {(1)} _ {z} \sigma ^ {(2)} _ {z} $$

上述观测作用于贝尔态的四个基状态得到的期望分别为 $+1, +1, +1, -3$，恰好对应于这个观测的四个特征值。

密度矩阵与约化密度矩阵 ¶

密度矩阵是描述量子系统的重要工具，可以用于估计观测结果，与经典系统的概率论相对应。

• 纯态 $\ket{\psi}$ 的密度矩阵为 $\rho \equiv \ket{\psi} \bra{\psi}$，混合态的密度矩阵为 $\rho = \sum _ {i} \text{P} _ i \ket{\psi _ {i}} \bra{\psi _ {i}}$
• 观测 $L$ 作用于量子态的期望可以通过相应的密度矩阵计算得到，$\braket{L} = \text{Tr} (\rho L)$，对于纯态和混合态均适用；其中，$\text{Tr}$ 表示矩阵求迹，定义为 $\text{Tr} (L) = \sum _ {i} \braket{i | L | i}$

密度矩阵具有如下性质：

• 密度矩阵都是厄米的，即 $\rho _ {ij} = \rho _ {ji} ^ *$
• 密度矩阵的迹均为 1，即 $\text{Tr} (\rho) = 1$
• 密度矩阵的特征值均为介于 0 和 1 之间的正数

约化密度矩阵是描述多量子比特系统的子系统的工具，可以用于估计仅作用于子系统的观测结果。对于 two-qubit 系统，记两个 qubit 分别表示子系统 A 和 B，则描述子系统 A 的约化密度矩阵为 $\rho _ {A} = \text{Tr} _ {B} (\rho)$，观测期望为 $\braket{L _ {A}} = \text{Tr} _ {A} (\rho _ {A} L _ {A})$。注意，其中 $\text{Tr} _ {A}$ 表示矩阵求部分迹，且基于约化密度矩阵的期望并非常数，而是一个更低维的矩阵。

• 对于直积态 $\ket{\psi} = \ket{\lambda} _ {A} \ket{\phi} _ {B}$，子系统 A 的约化密度矩阵为 $\rho _ {A} = \text{Tr} _ {B} (\rho) = \ket{\lambda} \bra{\lambda}$，注意到 $\text{Tr} (\rho _ {A} ^ 2) = \text{Tr} (\rho _ {A}) = 1$，故子系统 A 是纯态
• 对于纠缠态，纯的纠缠态可以写作 $\ket{\psi} = \sum _ i c _ i \ket{\lambda _ i} _ A \ket{\phi _ i} _ B$，子系统 A 的约化密度矩阵为 $\rho _ {A} = \text{Tr} _ {B} (\rho) = \sum _ i | c _ i | ^ 2 \ket{\lambda _ i} \bra{\lambda _ i}$，注意到 $\text{Tr} (\rho _ A) = 1$，但 $\text{Tr} (\rho _ A ^ 2) = \text{Tr} (\rho _ B ^ 2) \not = 1$，故子系统 A 是混合态

类似于香农熵可以描述信息量，为描述由 A 和 B 两个子系统构成的纠缠系统，可以定义纠缠熵：

$$ S _ A \equiv - \text{Tr} _ A (\rho _ A \log _ 2 \rho _ A) = - \sum _ i | c _ i | ^ 2 \log _ 2 | c _ i | ^ 2 \;,\;\; S _ A = S _ B $$

纯态与混合态 ¶

纯态是经过充分的观测后被完全确定的量子态，而混合态是一系列纯态的统计学叠加。

• 纯态既可用狄拉克记号描述，也可用密度矩阵描述；而混合态只可用密度矩阵描述
• 对于纯态，有 $\rho ^ 2 = \rho ,\;\; \text{Tr} (\rho ^ 2) = 1$；对于混合态，有 $\rho ^ 2 \not = \rho ,\;\; \text{Tr} (\rho ^ 2) < 1$
• 在 Bloch 球中，球表面上的点表示纯态，球内部的点表示混合态

此外，为了进一步理解为什么“概率幅不是经典系统的概率论的量子对应，但密度矩阵是”，我们考虑构建一个 50%-50% 的叠加态：

• 考虑纯态 $\ket{\psi} = \frac{1}{\sqrt{2}} \ket{0} + \frac{1}{\sqrt{2}} \ket{1}$，其中两个基态的概率幅相等，但 $\ket{\psi}$ 事实上并不是一个 50%-50% 的叠加态，因为 $\ket{0}$ 和 $\ket{1}$ 存在相互干涉。当我们考察密度矩阵 $\rho = \ket{\psi} \bra{\psi} = \frac{1}{2} \ket{0} \bra{0} + \frac{1}{2} \ket{0} \bra{1} + \frac{1}{2} \ket{1} \bra{0} + \frac{1}{2} \ket{1} \bra{1}$ 或者观测期望 $\braket{A} = \frac{1}{2} \braket{0 | A | 0} + \frac{1}{2} \braket{0 | A | 1} + \frac{1}{2} \braket{1 | A | 0} + \frac{1}{2} \braket{1 | A | 1}$ 时，可以明显注意到结果的中间有两个 $\ket{0}$ 和 $\ket{1}$ 的相干项
• 考虑混合态 $\rho = \frac{1}{2} \ket{0} \bra{0} + \frac{1}{2} \ket{1} \bra{1}$，事实上这才是我们想要的 50%-50% 的叠加态，两个基态之间并不相干，因此可以直接使用经典系统概率论的加法原理进行叠加。当我们考虑观测期望 $\braket{A} = \frac{1}{2} \braket{0 | A | 0} + \frac{1}{2} \braket{1 | A | 1}$ 时，也可以明显注意到结果中并不存在相干项

量子系统的含时演化 ¶

含时演化 ¶

量子系统的含时演化是确定的、可逆的，有别于不确定的、不可逆的观测行为。

• 含时演化可由一个酉矩阵描述：$\ket{\psi (t)} = U(t) \ket{\psi (0)}$，其中 $U(t)$ 为含时演化算子
• 含时演化遵循薛定谔方程： $i\hbar \frac{\partial}{\partial t} \ket{\psi (t)} = H \ket{\psi (t)}$，其中 $H$ 为哈密顿量
• 密度矩阵 $\rho = \sum _ {i} \text{P} _ i \ket{\psi _ i} \bra{\psi _ i}$ 的含时演化结果可以描述为 $\rho ^ {\prime} = U \rho U ^ {+}$，其中 $\ket{\psi _ i ^ {\prime}} = U \ket{\psi _ i}$

通常而言，我们通过实验测量、理论推导等方式得到量子系统的哈密顿量，从而计算量子系统如何随着时间发生演化。如果哈密顿量与时间无关，则薛定谔方程显然有解 $\ket{\psi (t)} \equiv U(t) \ket{\psi (0)} = e ^ {-iHt / \hbar} \ket{\psi (0)}$。

Rabi 振动 ¶

对于处在磁场 $\vec{B}$ 中的 qubit，哈密顿量可由 $H = -\sigma \cdot \vec{B}$ 计算得到。取磁场为 $\vec{B} = B _ z \hat{z} + B _ 1 (\cos \omega t \hat{x} - \sin \omega t \hat{y})$，则哈密顿量为：

$$ H(t) = - \frac{\hbar \omega _ 0}{2} \sigma _ z - \frac{\hbar \omega _ 1}{2} (\sigma _ x \cos \omega t - \sigma _ y \sin \omega t) $$

旋转参考系使得哈密顿量与时间无关：

$$ H ^ {\prime} = - \frac{\hbar (\omega _ 0 - \omega)}{2} \sigma _ z - \frac{\hbar \omega _ 1}{2} \sigma _ x $$

取 $\ket{\psi (0)} = \ket{0}$，则在时间 $t$ 时量子态处于 $\ket{1}$ 的概率是：

$$ |\braket{1 | \psi (t)}| ^ 2 = |\braket{1 | e ^ {-iH ^ {\prime}t / \hbar} | 0}| ^ 2 = (\frac{\omega _ 1}{\Omega}) ^ 2 \sin ^ 2 \frac{\Omega t}{2} $$

其中，$\Omega = \sqrt{(\omega - \omega _ 0) ^ 2 + \omega _ 1 ^ 2}$；注意这里推导的关键一步是变换 $\exp (i\frac{\theta}{2} \sigma \cdot \hat{n}) = I \cos \frac{\theta}{2} + i (\sigma \cdot \hat{n}) \sin \frac{\theta}{2}$。

量子电路 ¶

量子逻辑门 ¶

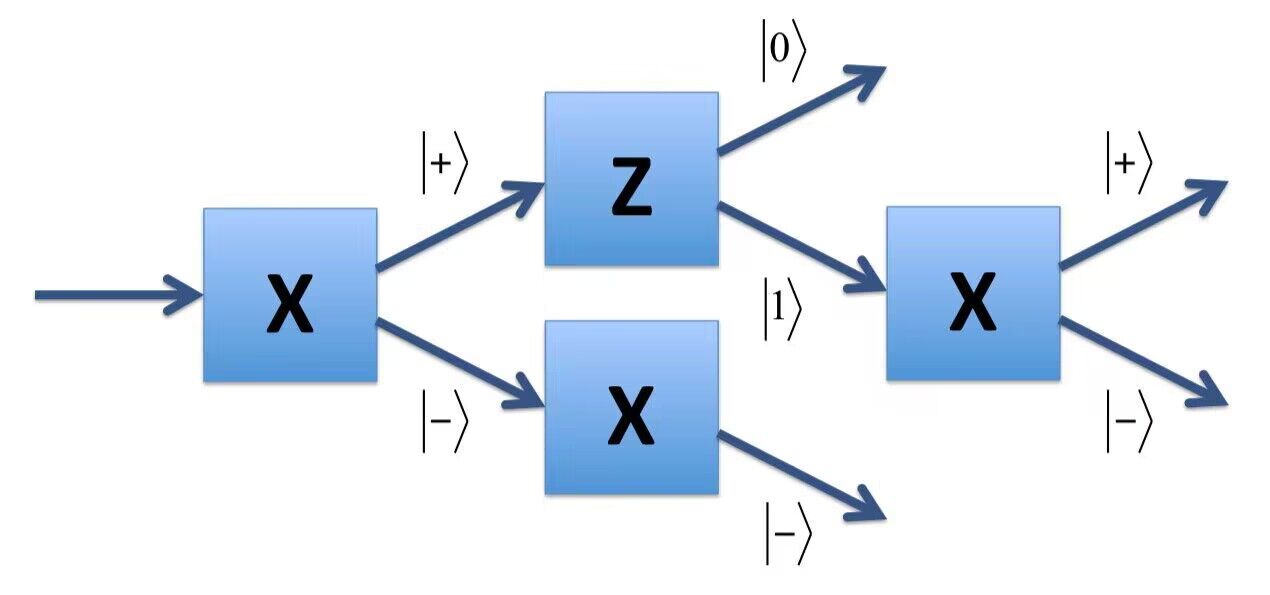
量子电路由量子逻辑门组成，每个量子门都相当于一个可逆算子。

• 泡利 X 门，$X = \begin{pmatrix} 0 & 1 \cr 1 & 0 \end{pmatrix}$，将 $\ket{0}$ 和 $\ket{1}$ 量子态互相翻转，故又称非门
• 泡利 Z 门，$Z = \begin{pmatrix} 1 & 0 \cr 0 & -1 \end{pmatrix}$，保持 $\ket{0}$ 不变，并将 $\ket{1}$ 映射成 $-\ket{1}$
• 哈达玛门，$H = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \cr 1 & -1 \end{pmatrix}$，使得 $H \ket{0} = \frac{1}{\sqrt{2}} (\ket{0} + \ket{1})$，$H \ket{1} = \frac{1}{\sqrt{2}} (\ket{0} - \ket{1})$，常用于量子并行化
• $\pi / 4$ 门，$S = \begin{pmatrix} 1 & 0 \cr 0 & i \end{pmatrix}$
• $\pi / 8$ 门，$T = \begin{pmatrix} 1 & 0 \cr 0 & e ^ {i\pi / 4} \end{pmatrix}$
• 受控非门（CNOT），作用于双量子位，当控制量子位为 $\ket{1}$ 时，对受控量子位执行非门，否则不做任何操作

标准的逻辑完备量子门由 H、S、T、CNOT 门组成，能够无限趋近地实现量子计算中的任意酉算子。

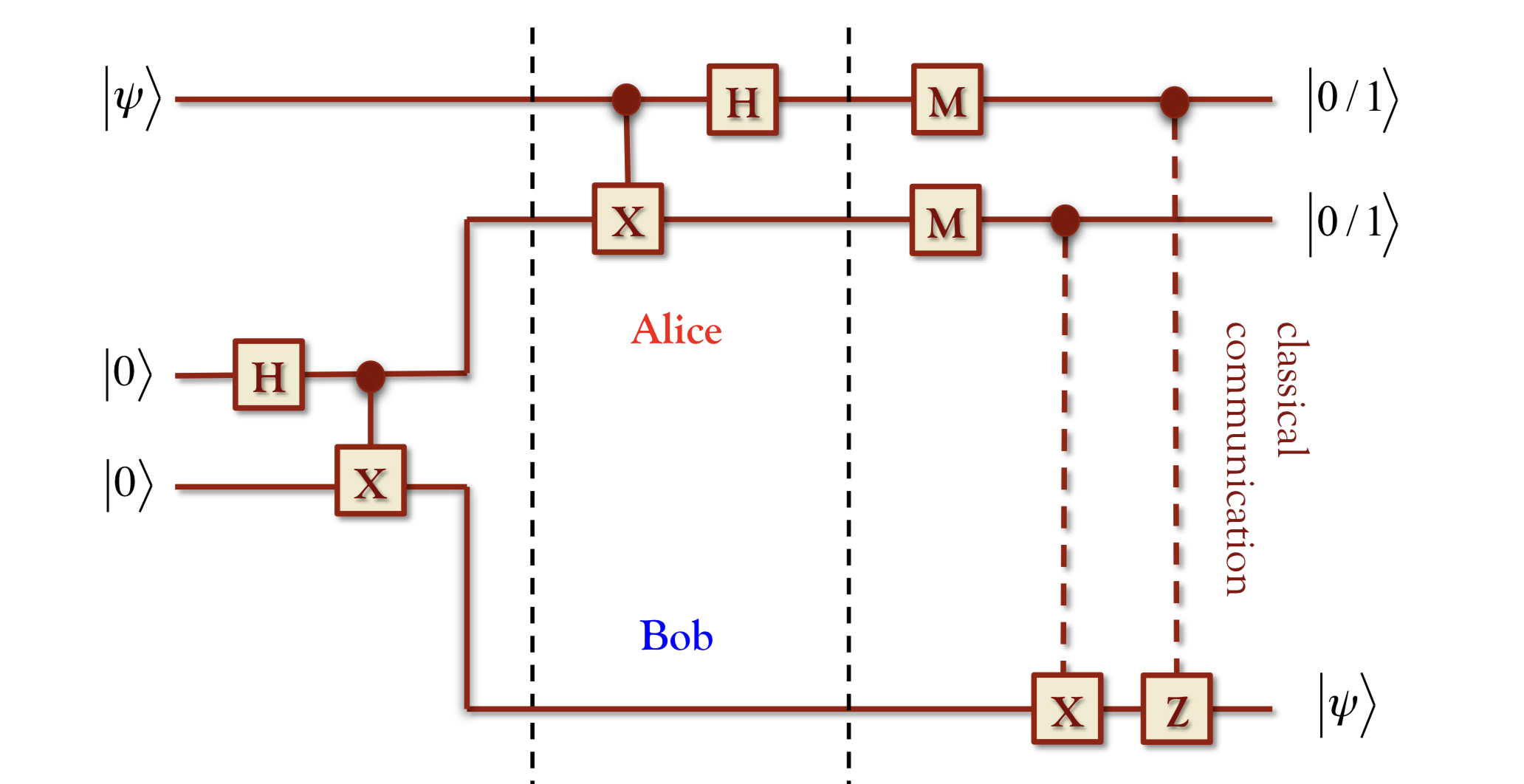
量子隐形传态 ¶

量子隐形传态是一种将量子态传送至任意距离的技术。

• 量子隐形传态不是克隆，在接收端重构出量子态前，发送端的量子态一定已经坍缩，并不违背不可克隆原理
• 量子隐形传态不能超光速，因为发送端必须使用经典信道传递一定信息给接收端

下面分析一个量子隐形传态的简单模型：假设 Alice 拥有一个量子态 $\ket{\psi} = a \ket{0} + b \ket{1}$，但她并不需要知道这个量子态具体是什么（不需要知道参数 $a$ 和 $b$），她的目标是使这个量子态能够被任意远处的 Bob 重构出来。

首先准备贝尔态 $\ket{\Omega} = \frac{1}{\sqrt{2}} (\ket{00} + \ket{11})$ 并将这两个纠缠的量子比特分发给 Alice 和 Bob，此时整个系统的量子态可以写作：

$$ \begin{aligned} \ket{\Psi} &= (a\ket{0} + b\ket{1}) \otimes \frac{1}{\sqrt{2}} (\ket{00} + \ket{11}) \cr &= \frac{1}{\sqrt{2}} (\ket{00} + \ket{11}) (a\ket{0} + b\ket{1}) + \frac{1}{\sqrt{2}} (\ket{01} + \ket{10}) (a\ket{1} + b\ket{0}) \cr &+ \frac{1}{\sqrt{2}} (\ket{00} - \ket{11}) (a\ket{0} - b\ket{1}) + \frac{1}{\sqrt{2}} (\ket{01} - \ket{10}) (a\ket{1} - b\ket{0}) \end{aligned} $$

随后，Alice 对自己的两个量子比特进行反变换（CNOT、H 门），此时整个系统的量子态为：

$$ \begin{aligned} \ket{\Psi} &= \frac{1}{2} \ket{00} (a\ket{0} + b\ket{1}) + \frac{1}{2} \ket{01} (a\ket{1} + b\ket{0}) + \frac{1}{2} \ket{10} (a\ket{0} - b\ket{1}) + \frac{1}{2} \ket{11} (a\ket{1} - b\ket{0}) \cr &= \frac{1}{2} (\ket{00} I + \ket{01} X + \ket{10} Z + \ket{11} XZ) (a\ket{0} + b\ket{1}) \end{aligned} $$

也就是说，Alice 此时可以通过观测自己的两个量子比特，来判断出 Bob 的那个量子比特的状态，从而通过经典信道通知 Bob 执行相应的操作，并最终使 Bob 的那个量子比特演化成 $a\ket{0} + b\ket{0}$。注意到此时由于观测，Alice 处的 $\ket{\psi}$ 已经坍缩，整个过程其实是 $\ket{\psi}$ 在 Alice 处消解，随后又在 Bob 处重构。事实上，量子隐形传态传递的并不是量子态 $\ket{\psi}$ 本身，而是量子态蕴含的信息 $a$ 和 $b$。