跳转至

算法分析

约 551 个字 49 行代码 预计阅读时间 3 分钟

回溯

  • 回溯法用于寻找某些计算问题（尤其是约束满足问题）的解决方案，是一种更高效的暴力枚举
  • 回溯法在隐式的搜索树上执行深度优先搜索，对每个节点进行评估，当没有必要继续向下搜索时果断放弃该节点及其子树（剪枝）
  • 回溯法遍历的实际树只是整棵搜索树的一部分，回溯法的效率与数据规模、剪枝策略、实际树的大小与形态有关，复杂度分析通常较难完成

回溯法有许多经典案例，比如八皇后问题和下面用伪代码展示的收费公路重建问题：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
bool backtracking(int i) {
    bool found = false;
    if (i > N) return true; /* solved with X[1]...X[N] */
    for (each X[i] in S[i]) {
        /* check if satisfies the restriction R */
        ok = check(X, R);            /* pruning */
        if (ok) {
            count X[i] in;
            found = backtracking(i+1);
            if (!found) undo(i); /* backtrack to X[1]...X[i-1] */
        }
        if (found) break;
    }
    return found;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
bool reconstruct(DistType[] X, DistSet D, int N, int left, int right) {
    /* X[1]...X[left-1] and X[right+1]...X[N] are solved */
    bool found = false;
    if (isEmpty(D)) return true;
    maxD = findMax(D);
    /* option 1: X[right] = maxD */
    /* check if every |maxD-X[i]| is in D for all X[i]'s that have been solved */
    ok = check(maxD, N, left, right);
    if (ok) {
        X[right] = maxD;
        for (i = 1; i < left; i++)     delete(|X[right]-X[i]|, D);
        for (i = right+1; i <= N; i++) delete(|X[right]-X[i]|, D);
        found = reconstruct(X, D, N, left, right-1);
        if (!found) { /* backtrack */
            for (i = 1; i < left; i++)     insert(|X[right]-X[i]|, D);
            for (i = right+1; i <= N; i++) insert(|X[right]-X[i]|, D);
        }
    }
    /* option 2: X[left] = X[N] - maxD */
    if (!found) {
        ok = check(X[N]-maxD, N, left, right);
        if (ok) {
            X[left] = X[N] - maxD;
            for (i = 1; i < left; i++)     delete(|X[left]-X[i]|, D);
            for (i = right+1; i <= N; i++) delete(|X[left]-X[i]|, D);
            found = reconstruct(X, D, N, left+1, right);
            if (!found) { /* backtrack */
                for (i = 1; i < left; i++)     insert(|X[left]-X[i]|, D);
                for (i = right+1; i <= N; i++) insert(|X[left]-X[i]|, D);
            }
        }
    }
    return found;
}

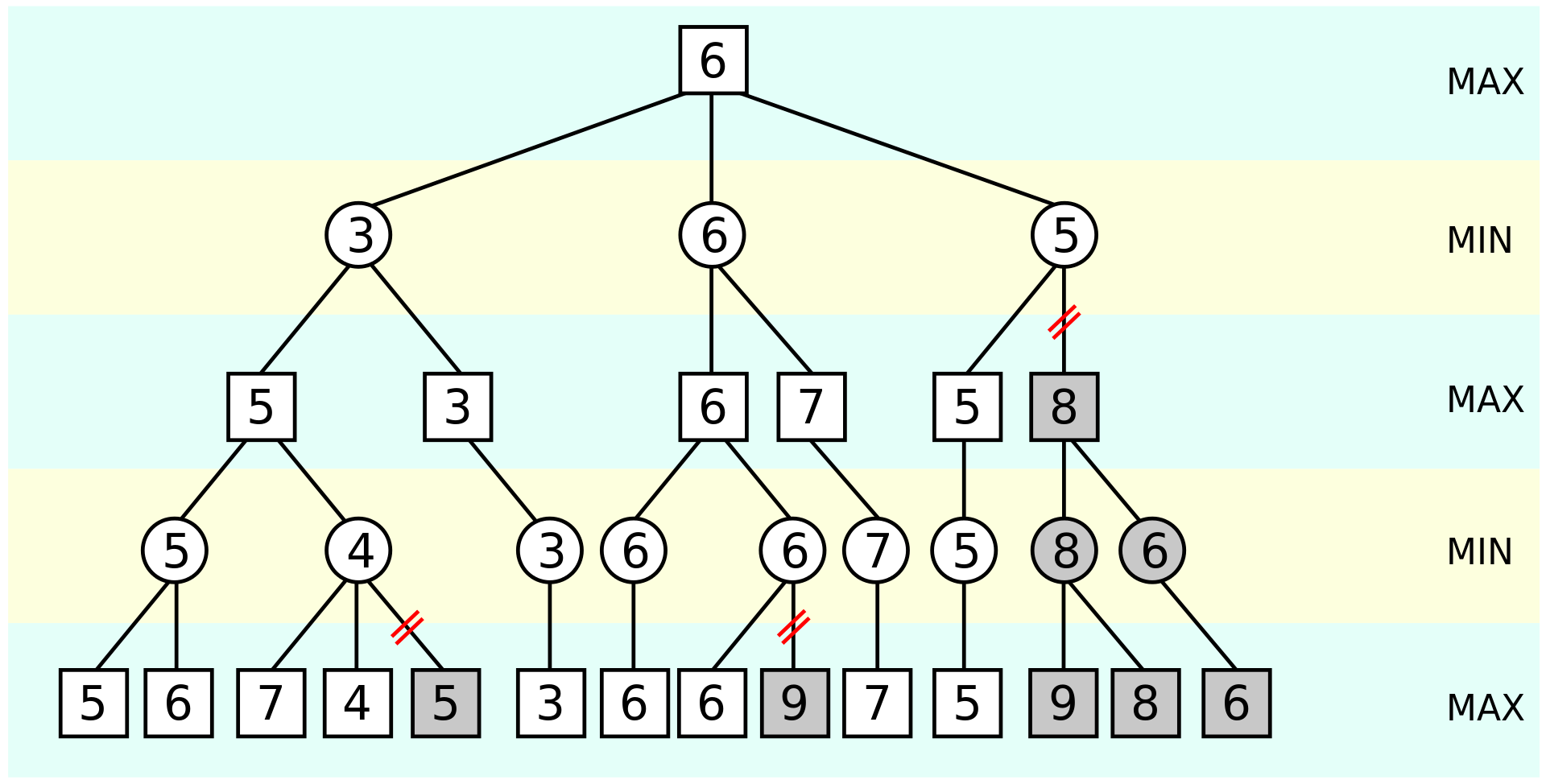
$\alpha$-$\beta$ 剪枝

  • $\alpha$-$\beta$ 剪枝是一种对抗性搜索算法，常用于双人对弈游戏
  • 右图的博弈树可以代表一个双人零和游戏，每个节点都对应一个效用函数
  • $\alpha$ 剪枝就是最大化玩家总是要最大化对手最小化的效用，$\beta$ 剪枝就是最小化玩家总是要最小化对手最大化的效用

分治

  • 分治法递归地将问题分解成多个同类子问题，直到问题变得足够简单，然后把子问题的解决方案合并以给出原问题的解决方案
  • 分治法时间复杂度求解方法有，先猜后证（注意常数项必须保持）、递归树法（每层的合并复杂度 + 最小子问题的复杂度），以及许多相关定理

主定理

假设有递推关系 $T(n)=aT(\frac{n}{b})+f(n)$，则：

  • 如果存在正的常数 $\epsilon$，使得 $f(n)=\Omicron(n^ {\log_{b}a-\epsilon})$，则 $T(n)=\Theta(n^ {\log_{b}a})$
  • 如果存在非负常数 $\epsilon$，使得 $f(n)=\Omega(n^ {\log_{b}a+\epsilon})$，且存在常数 $c<1$ 使得对于充分大的 $n$ 有 $af(\frac{n}{b})\leq cf(n)$，则 $T(n)=\Theta(f(n))$
  • 如果存在非负常数 $k$，使得 $f(n)=\Theta(n^ {\log_{b}a}\log^ {k}n)$，则 $T(n)=\Theta(n^ {\log_{b}a}\log^ {k+1}n)$

理解主定理的关键在于比较 $n ^ {\log_{b}a}$ 和 $f(n)$，前者大则最小子问题复杂度占主导，后者大则合并复杂度占主导。

下面给出比主定理更强的结论，实际上补充了主定理的第二、三条，假设有递推关系 $T(n) = aT(n/b) + \Theta(n ^ k \log ^ p n)$，其中 $a \geq 1, b > 1, k \geq 0$ 且 $p$ 为任意实数，则：

  • 若 $a > b ^ k$，则 $T(n) = \Theta(n ^ {\log_{b}a})$
  • 若 $a < b ^ k$，则：
    • 若 $p \geq 0$，$T(n) = \Theta(n ^ k \log ^ p n)$
    • 若 $p < 0$，$T(n) = \Theta(n ^ k)$
  • 若 $a = b ^ k$，则：
    • 若 $p > -1$，$T(n) = \Theta(n ^ k \log ^ {p+1} n)$
    • 若 $p = -1$，$T(n) = \Theta(n ^ k \log \log n)$
    • 若 $p < -1$，$T(n) = \Theta(n ^ k)$

动态规划

最后更新: 2024年4月23日 10:51:39
创建日期: 2024年3月12日 20:05:28