信号处理 ¶

锋电位分类 ¶

用于 BCI 的侵入式技术通常依赖于由微电极阵列记录到的锋电位，这些信号通常是电极附近数个神经元所产生的神经混合信号。传统的 BCI 输入信号形式期望是来自单个神经元的锋电位，所以需要通过锋电位分类将单个神经元产生的锋电位从混合信号中提取出来。

锋电位分类具有以下几种常用方法：

• 依据幅值幅度的分类
• 窗型鉴别器（人工）
• 自动归类（最新的趋势），依据锋电位波形的特征（特征提取方法：小波分析、主成分分析等）

频域分析 ¶

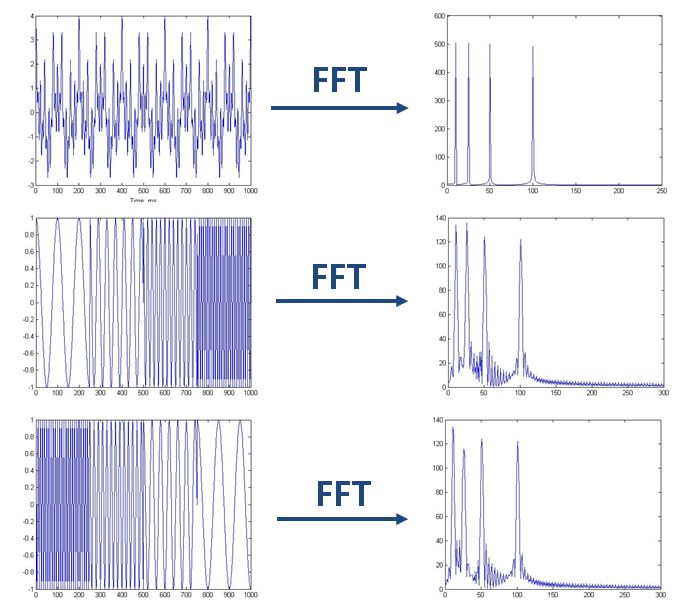
诸如 EEG 的非侵入式技术基于能反映数千个神经元活动的信号，这些信号能捕捉具有特定频率范围的“脑电波”，因此对信号进行频域分析特别有用。

傅里叶分析 ¶

傅里叶分析的基本思想是将一个信号分解为不同频率的正弦和余弦波的加权和，幅值 $a_n$ 和 $b_n$ 能由输入信号计算得到。信号分解使我们可以进行基于频率的多种类型的滤波处理。

离散傅里叶变换 ¶

BCI 应用中，通常是在离散时间间隔对大脑信号进行采样，相应的可以使用离散傅里叶变换（DFT）。

许多 BCI 系统从一段时间间隔内大脑信号的功率谱中提取特征，计算信号的功率谱 $P(n)$ 即计算信号幅值的平方。

快速傅里叶变换 ¶

DFT 的时间复杂度为 $O(T^2)$ ，当数据量较大时运算速度很不理想。快速傅里叶变换（FFT）是计算 DFT 的一种更高效的方法，时间复杂度为 $O(T\log T)$ 。

最通用的 FFT 算法是Cooley-Tukey FFT算法，采用了“分而治之”的策略，用递归的方法将一个 DFT 分成许多更小型的 DFT。

FFT 是将时变信号变换到频域的最常用方法。

小波分析 ¶

自然界的信号几乎都是非平稳的，但是傅里叶变换处理非平稳信号时效果较差，它只能获取信号总体上包含哪些频率的成分，但是对各成分出现的时刻并无所知。

一种简单可行的优化方法是加窗，在短时窗内（近似平稳）进行傅里叶分析，这就是短时傅里叶分析（STFT）。但是 STFT 在选择窗口宽度时很难协调时间分辨率和频率分辨率之间的矛盾。

小波变换（WT）可以更好地解决这一问题。

小波变换的基函数不再是正弦和余弦函数，而是有限长的会衰减的小波基。小波函数由一个母小波通过伸缩和平移得到。尺度 $\alpha$ 控制小波函数的伸缩，平移量 $\tau$ 控制小波函数的平移，尺度对应频率，平移量对应时间。

$$ WT(\alpha, \tau) = \frac{1}{\sqrt[]{\alpha}} \int_{-\infty}^{+\infty} {f(t) \times \psi(\frac{t-\tau}{\alpha}) dt} $$

小波分析信号处理不仅可以知道信号由怎样频率的成分，而且知道其在时域上对应的具体位置。傅里叶变换只能得到一个频谱，而小波变换可以得到一个时频谱。

此外，小波变换在处理突变信号时也优于傅里叶变换，因为傅里叶变换存在吉布斯效应，对突变信号的拟合效果不够理想。

但是，小波分析的难点在于寻找母小波（尺度函数），这是构造小波变换的关键所在。

时域分析 ¶

Hjorth 参数 ¶

Hjorth 参数对于计算时变信号的三个重要特征提供了一种快速的方法，这三个特征为：平均功率、均方根频率以及均方根频率展开。

基于方差的 Hjorth 参数比其他方法拥有更快的计算速度，因而其在 EEG 分析中应用得十分普遍，适用于需要快速持续地获取时变信号特征的应用场合。

分形维数 ¶

一般来说，如果一个信号表现出自相似性，则认为它是分形的。分形维数是对这种相似性的定量测量。常用于大脑信号（尤其是 EEG）的分形维数测量基于Higuchi提出的方法。

这种方法产生的分形维数 D 在 1~2 之间，对于简单曲线（例如平坦），D 接近于 1，对于遍布整个二维平面的高度不规则曲线，D 接近于 2。

诸如 EEG 的大脑信号的分形维数 D 一般在 1.4~1.7 之间，值越大表明发生了高锋电位的活动，例如癫痫。在典型的 BCI 应用中，使用滑窗计算 D 值，并将其用于描绘时变脑信号“复杂度”的局部特征。

自回归模型 ¶

自回归模型（AR）基于这样的事实：自然信号在时间上有相关联的趋势，因此常常能够利用之前的一些测量值来预测下一个测量值。

传统的 AR 模型基于之前的测量值并利用一组系数 $a_i$ 来预测当前的信号值 $x_i$ ：

$$ x_i = \sum_{i=1}^p a_i x_{t-i} + \epsilon $$

传统的 AR 模型假设信号的统计特性是平稳的，但是大脑信号是非平稳的，因而需要一组时变的系数 $a_{i, t}$ ，这就产生了自适应自回归（AAR）模型：

$$ x_i = \sum_{i=1}^p a_{i, t} x_{t-i} + \epsilon _t $$

用卡尔曼滤波等方法可以实时更新时变系数 $a_{i, t}$ 。由于系数随时间而变化，它包含了信号的局部统计结构，在 BCI 中可以用作进一步处理的特征。

贝叶斯滤波 ¶

前面讨论的时域方法不能明确保持对在时域计算的信号特性的不确定性估计。在 BCI 中，保持对信号不确定性的表示是很重要的。贝叶斯滤波技术提供了一种对信号特性及其不确定性进行估计的统计上合理的方法。

首先给出概率与统计学中一条重要的定理，即贝叶斯定理（贝叶斯法则）：

$$ P(x|y) = \frac{P(y|x) P(x)}{P(y)} $$

其中，$P(x|y)$ 称为给定 $y$ 条件下 $x$ 的后验概率，$P(y|x)$ 称为似然函数，$P(x)$ 是 $x$ 的先验概率。

贝叶斯定理对信号特性的统计估计有着深远的影响，因为它指出了测量值 $P(y|x)$ 如何能与先验知识 $P(x)$ 相结合。以 EEG 为例，$y$ 为 EEG 测量值，$x$ 为可引起大脑反应的刺激，先验概率 $P(x)$ 可由实验员事先给定。研究人员感兴趣的是找到产生测量到的 EEG 信号的原因，这就相当于估计后验概率 $P(x|y)$ 。

然后我们通过一堆噼里啪啦的分析即可得到一般形式的贝叶斯滤波（更新规则）：

$$ P(x_t|y_1,\cdots,y_t) = \alpha P(y_t|x_t) \sum_{x_{t-1}} P(x_t|x_{t-1}) P(x_{t-1}|y_1,\cdots,y_{t-1}) $$

$$ \alpha = 1/P(y_t|y_1,\cdots,y_{t-1}) $$

贝叶斯滤波器说明了应如何将新的测量值 $y_t$ 与之前的后验概率 $P(x_{t-1}|y_1,\cdots,y_{t-1})$ 相结合，以求得 $t$ 时刻后验概率的分布。常用的统计滤波方法，如卡尔曼滤波和粒子滤波，都是上式的特殊情况。

在更一般的情况下，贝叶斯滤波可以被认为是在动态贝叶斯网格（DBN）中做概率推断。DBN 是一种图模型，其中的节点代表随机变量（即前文中的状态 $x_t$ 和观测值 $y_t$），从一个节点到另一个节点的箭头代表条件概率（即前文中的 $P(x_t|x_{t-1})$ 和 $P(y_t|x_t)$）。

卡尔曼滤波 ¶

卡尔曼滤波器是贝叶斯滤波中最知名的算法，它是在假设动态概率和测量概率均为线性高斯模型的基础上导出的。

卡尔曼滤波器可简化为如下所示的方程来递归更新每个 $t$ 时刻下的均值 $\hat x_t$ 和协方差 $S_t$ ：

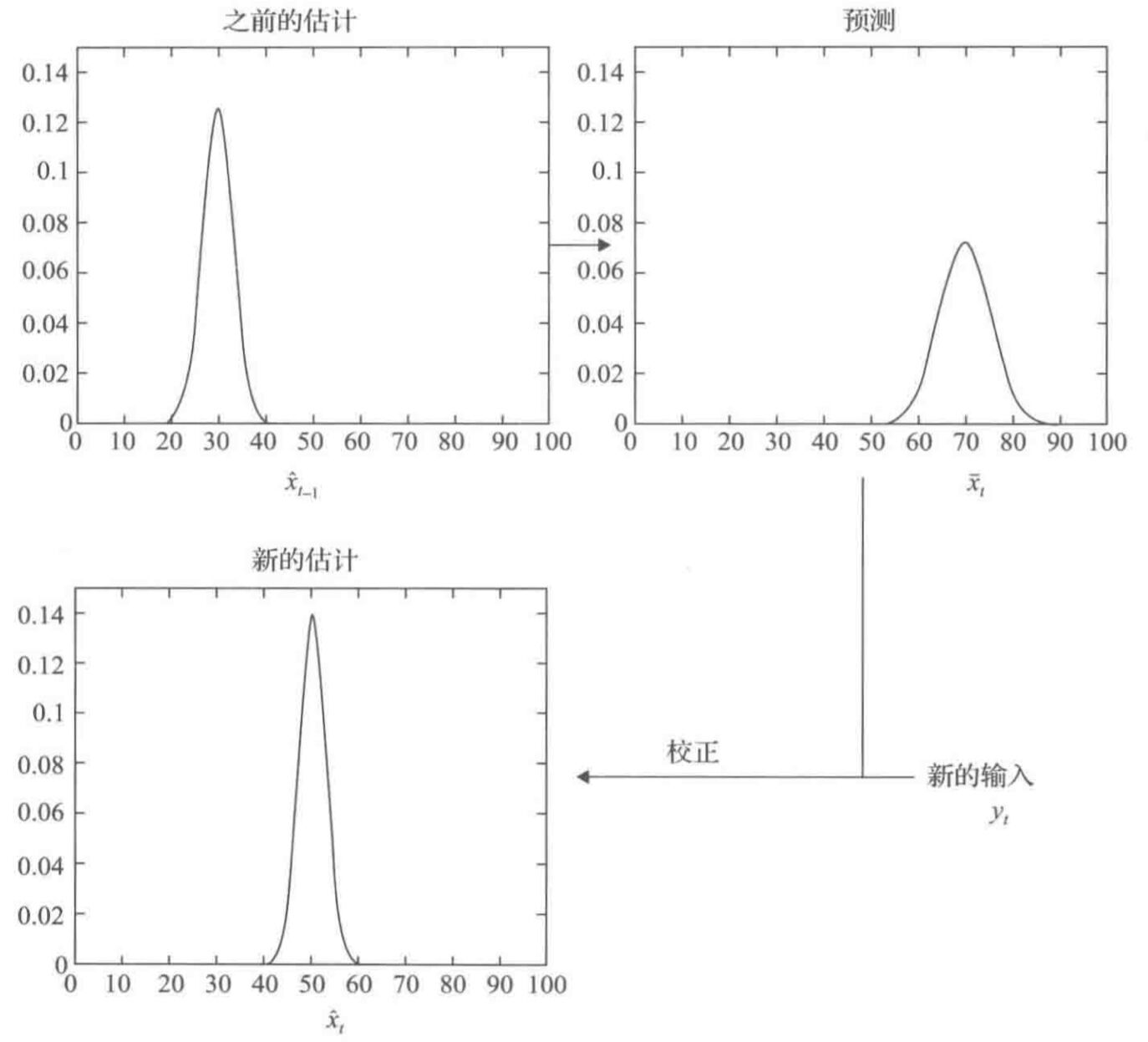
卡尔曼滤波器将环境的隐藏状态都估计为用均值和方差（协方差）定义的高斯分布。其工作过程为：在测量 $y_t$ 之前，先预测均值 $\overline x_t$ 和协方差 $M_t$ ，它们由卡尔曼滤波器在 $t-1$ 时刻估计的均值和协方差计算得到，然后计算预测误差 $(y_t - B \overline x_t)$ ，将校正项 $K_t (y_t - B \overline x_t)$ 与之前的预测均值 $\overline x_t$ 相加即可得到新的估计值 $\hat x_t$ 。下图说明了卡尔曼滤波器的预测 - 校正周期：

粒子滤波 ¶

卡尔曼滤波器假设其动态和测量过程为线性的，并服从高斯分布。基于这种简化的假设能导出贝叶斯滤波中更新方程的解析表达式，但在许多实际情况下这种假设可能并不适用。

粒子滤波是一种适用于分析非线性非高斯过程的方法。粒子滤波通过一群样本（粒子）来逼近后验概率 $P(x_t|y_1,\cdots,y_t)$ ，具体过程是“测量 - 加权 - 重采样 - 预测”的周期重复。

当样本数趋于无穷大时，粒子滤波算法计算出的样本能正确表示后验概率 $P(x_t|y_1,\cdots,y_t)$ 。实际上，使用的样本数取决于特定的应用及可获得的计算能力，样本数一般在 1000~5000 之间。

空间滤波 ¶

空域滤波将不同位置（通道，channel）记录的大脑信号通过几种方式进行信号转换。下面讨论一些常用的空域滤波方法。

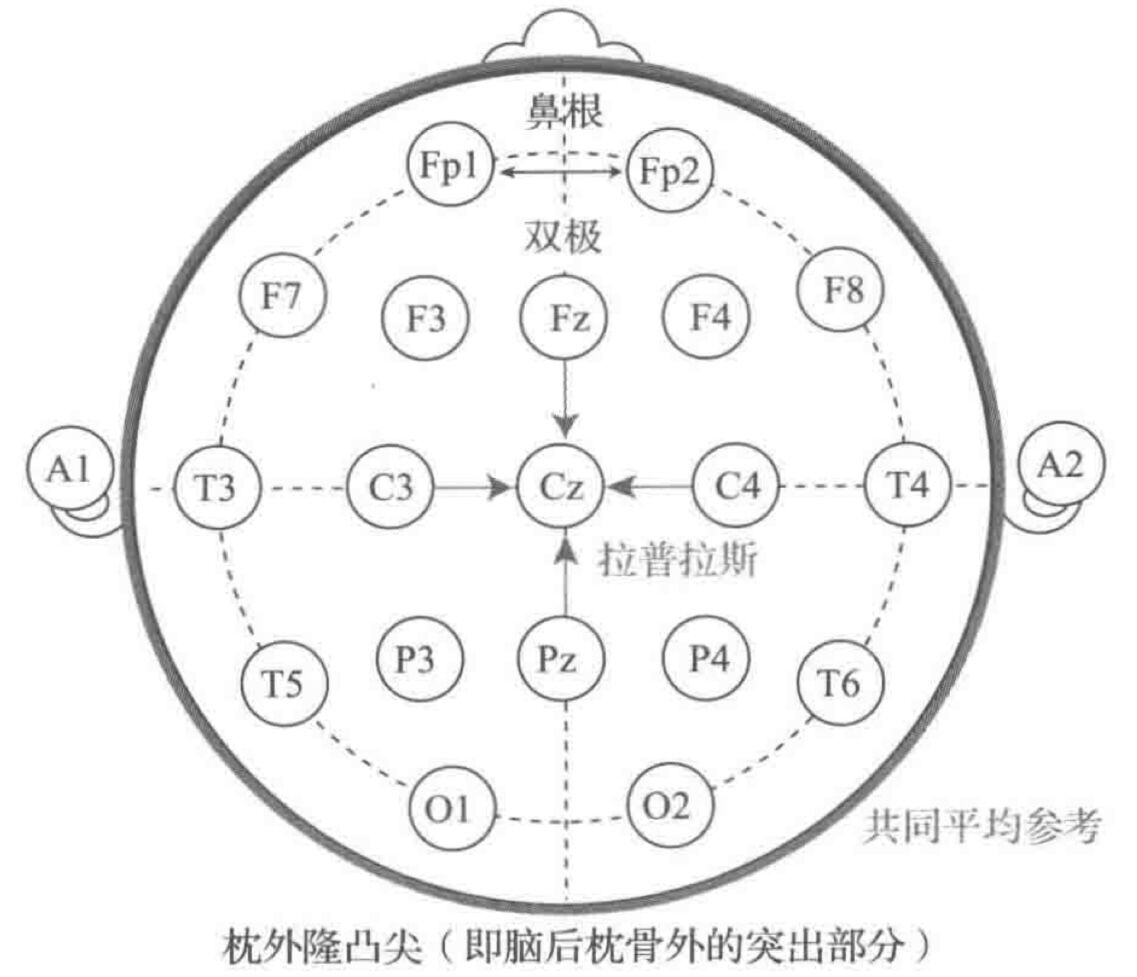
双极、拉普拉斯和共同平均参考 ¶

• 双极滤波： 计算双极信号 $\widetilde s_{i,j}=s_i-s_j$ ，用以突显两个感兴趣的电极（第 $i$ 通道和第 $j$ 通道）之间的电位差。

• 拉普拉斯滤波： 用第 $i$ 个电极的信号减去四个正交的最近邻电极信号的平均值，用以去除所感兴趣的电极上存在的一些普遍活动，增强第 $i$ 个电极的局部活动。 $$ \widetilde s_i = s_i - \frac{1}{4} \sum_{i\in \theta} s_i $$

• 共同平均参考（CAR）： 用第 $i$ 个电极的信号减去其他所有信号的平均值，以增强第 $i$ 个电极上的局部活动。 $$ \widetilde s_i = s_i - \frac{1}{N} \sum_{i=1}^N s_i $$

三种基本的空间滤波技术示例

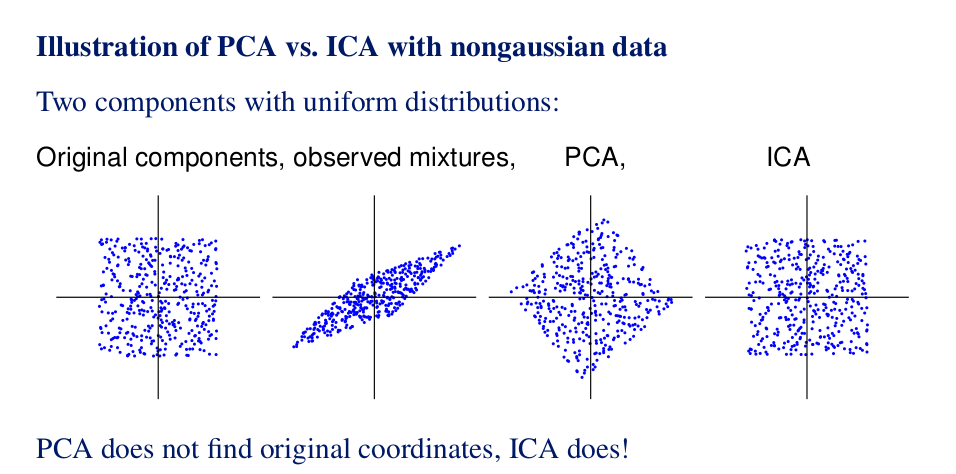
主成分分析 ¶

主成分分析（PCA）用于数据降维，实际上就是将在原有特征空间中分布的数据映射到新的维数更低的特征空间，实现降秩。具体而言，就是将原坐标旋转变换到最大方差的方向上，即使得在新坐标系中，某几根坐标轴上数据分布的方差较大，我们认为在这些特征（主成分）上，不同数据的区分度较高，如果原数据是冗余的，那么通过这种方法仅保留一些方差大的方向，舍弃方差小的方向，使数据维数显著降低。

PCA 的具体操作关键在于寻找数据方差最大的方向。运用线性代数的方法，可以通过计算数据协方差矩阵 $A$ 的特征向量来求解，最终得到一个低维且不相关的向量 $a$（$a$ 的维数小于等于输入 $x$ 的维数），该向量可以作为有效的“特征向量”用于 BCI 的分类或者其他类型的分析。

独立分量分析 ¶

独立分量分析（ICA）也是一种线性变换过程。但是PCA 只能保证变换后数据具有不相关性，但是无法保证其高阶独立性，而我们希望数据的各阶统计量都能利用。ICA 的目标就是寻找一种方法使得变换后的数据具有最强的独立性。

独立性是重要的，相比不相关性，独立性和真实的信号源关系密切。典型 BCI 中记录到的信号，是大脑中一组统计独立的信号源线性混合的结果，用 $x$ 表示记录到的信号， $y$ 表示隐含的独立源向量， $M$ 表示未知的混合矩阵。我们需要同时估计 $M$ 和 $y$ ，从而将 $y$ 还原。

$$ x = M y $$

$W$ 也称为解混矩阵，因为它试图将混合的源分离开。独立分量分析通过寻找解混矩阵来恢复隐含的源。当 $a$ 和 $x$ 矩阵大小相同时，最优的 $W = M^{-1}$ 。

$$ a = W x $$

目前存在多种计算 $W$ 的算法，其中最常用的是Bell-Sejnowski "infomax" 算法以及FastICA。由中心极限定理可得，独立源信号的线性混合几乎总是服从高斯分布，从而 ICA 算法将一个合适的非高斯分布作为待求的 $P(a_i)$ ，从得到的最优化函数推导出 $W$ 的估算准则。

无论是将 ICA 的输出向量 $a$ 作为分类的特征向量和用于分离出感兴趣的大脑节律信号，还是去除 EEG 中的肌电伪迹，ICA 被证明可用于 BCI 的多个组成部分。

共空间模式 ¶

共空间模式（CSP）是一种两分类任务下的空域滤波特征提取算法。

与 PCA 和 ICA 不同，CSP 是一种监督方法，即训练数据集被标记过，每个数据向量的类别是已知的。例如，大脑信号是在受试者执行两种不同的任务（手和脚的运动想象）时采集的。CSP 寻找合适的空间滤波器（线性代数过程，利用矩阵的对角化），使两类信号的方差值差异最大化，从而得到具有较高区分度的特征向量。

CSP 已经成为基于 EEG 的 BCI 的一种常用滤波方法，其实质上使得 BCI 所使用特征的可区分度最大化。

伪迹去除技术 ¶

下面介绍一些重要的伪迹去除方法：

• 阈值法： 通过设定阈值来舍弃任何受污染的数据。 阈值法的主要缺点在于并不是所有受污染的数据都应当被舍弃。

• 带阻和陷波滤波： 带阻滤波使信号中特定频带的分量得到衰减，而使其余分量通过。 具体操作上，首先将信号变换到频域，滤除选择的频带，并反变换回时域。常用的带阻滤波器的阻带设置在59 ~ 61Hz（美国），用于滤除电力工频噪声；另一种带阻滤波器的阻带设置在较低的频段（如1 ~ 4Hz），可以用于滤除EEG中的EOG伪迹；低通滤波有时也用于滤除EMG伪迹。 但是，只有当感兴趣的大脑信号频带与伪迹所处频带不同时，上述方法才适用。

• 线性模型： 伪迹对记录的大脑信号产生影响，对这些影响进行建模的一种简单方式是假设这些影响是可叠加的。 例如EEG中EOG伪迹的滤除： $$ EEG_i^{true} (t) = EEG_i (t) - K \cdot EOG(t) $$

• 主成分分析： PCA已被证明对于去除EEG中的EOG伪迹是有效的。 但是，在某些情况下，假设伪迹和大脑信号不相关可能并不合适，PCA可能不能用于分离这些伪迹和真实脑信号。

• 独立分量分析： ICA寻找的是数据之间的独立性而不是不相关性，从而克服了PCA的一些缺点。