自动机理论 ¶

前言 ¶

问题 ¶

• 四类问题：优化问题、搜索问题、判定问题、计数问题
  • 其中，判定问题（decision problem）是最简单的
• 如何证明一个问题是难的，是计算理论的一个核心问题
  • 如果能证明判定问题是难的，那么相应的其他问题也就都是难的，所以本门课程主要关注判定问题
• 判定问题的答案分为 yes-instance 和 no-instance
• 判定问题的定义是：给定一个字符串 $w$，判断 $w$ 是否属于集合 {encoding of yes-instance}

语言 ¶

• 字符集（alphabet）是一个有限的符号集合，字符串（string）是字符集上的有限的序列（sequence）
  • 字符集和字符串都可以是空的，空串用保留字 $e$ 表示
  • 字符串的长度用 $|w|$ 表示，$|e|=0$
  • 字符集 $\Sigma$ 上所有长度为 $i$ 的字符串的集合记为 $\Sigma ^ i$
  • 字符串 $\Sigma$ 上所有字符串的集合记为 $\Sigma ^ * = \bigcup _ {i\geq 0} \Sigma ^ i$，所有非空字符串的集合记为 $\Sigma ^ + = \bigcup _ {i\geq 1} \Sigma ^ i$
  • 字符串操作
    • concatenation：$|w _ 1 w _ 2| = |w _ 1| + |w _ 2|$
    • exponentiation：$|w ^ i| = i|w|$
    • reversal：$|w ^ R| = |w|$
• 语言（language）over $\Sigma$ 的定义是：任意 $\Sigma ^ *$ 的子集
• 判定问题和语言是等价的
  • 判定问题 $\Rightarrow$ 语言：给定一个判定问题，可以用其 {encoding of yes-instance} 定义一个语言
  • 判定问题 $\Leftarrow$ 语言：给定一个语言 $L$，可以定义一个判定问题为字符串 $w$ 是否属于集合 $L$

有限自动机 ¶

DFA¶

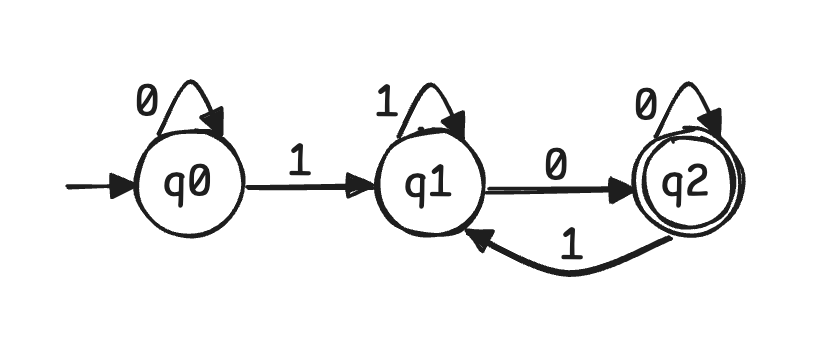
• 如图是一个确定性有限自动机（deterministic finite automata）
  • 其中，初始状态是唯一的，用单箭头指入表示，如 $q_0$；终止状态是若干的，用双圈表示，如 $q_2$
• DFA 的定义：$M = (K, \Sigma, \delta, s, F)$
  • $K$ 为有限的状态集合，$\Sigma$ 为字符集，$s$ 为初始状态，$F$ 为终止状态集合
  • $\delta$ 为转移函数，$\delta: K \times \Sigma \to K$
• 对于如图所示 DFA，考虑输入 $1010$，有 $(q _ 0, 1010) \vdash _ M (q _ 1, 010) \vdash _ M (q _ 2, 10) \vdash _ M (q _ 1, 0) \vdash _ M (q _ 2, e)$
  • 其中，记 configuration 为 $(q, w)$，表示当前状态 $q$ 和 剩余输入字符串 $w$
  • 其中，记 yield 为 $\vdash _ M$，表示单步转移，若 $w = aw ^ {\prime}$，$a \in \Sigma$ 且 $\delta(q, a)=q ^ {\prime}$，则 $(q, w) \vdash _ M (q ^ {\prime}, w ^ {\prime})$
  • 此外，可以用 $\vdash _ M ^ *$ 表示若干次的单步转移
• 接受逻辑
  • 自动机 $M$ 接受（accept）字符串 $w \in \Sigma ^ *$：$(s, w) \vdash _ M ^ * (q, e)$ 且 $q \in F$
  • 自动机 $M$ 接受（accept）语言 $L$：$M$ 接受所有属于 $L$ 的字符串，拒绝所有不属于 $L$ 的字符串
  • 注意，自动机 $M$ 接受的语言有且仅有一个，称为 the language of $M$，记为 $L(M) = \lbrace w \in \Sigma ^ *: M \; \text{accepts} \; w \rbrace$

NFA¶

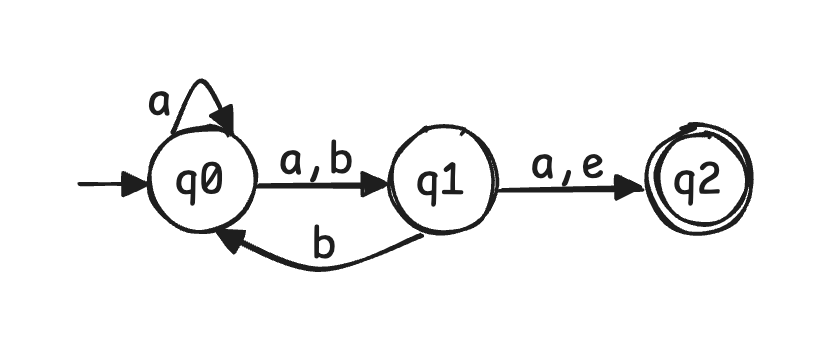
• 如图是一个非确定性有限自动机（non-deterministic finite automata），其与 DFA 的区别在于：
  • 一个状态在同一条件下可以有多种转移方案
  • 可以存在不消耗输入字符串的转移，即 $e$-transition
• NFA 的定义：$M = (K, \Sigma, \Delta, s, F)$
  • 其与 DFA 的区别在于转移方程不用函数描述，而是用更一般的关系（relation）描述
  • $\Delta$ 为转移关系，$\Delta \sube K \times (\Sigma \cup \lbrace e \rbrace) \times K$
• 接受逻辑与 DFA 同理
  • 注意，对于一个输入，NFA 可能存在多种路线，但只要其中一条路线被接受，就认为 NFA 接受该输入
  • 理解一：并行计算，出现多种转移方案时拷贝进程，只要其中一条进程走通，则程序走通
  • 理解二：NFA always makes the right guess
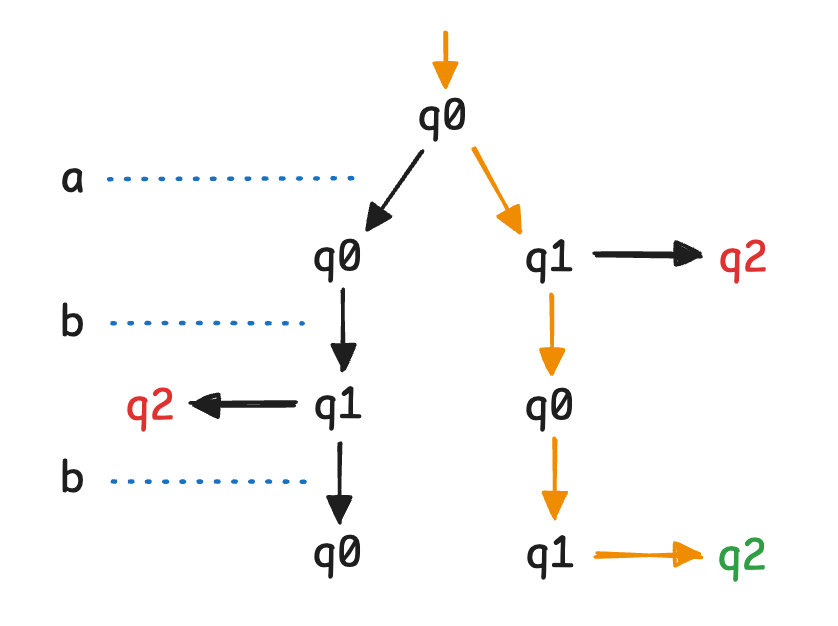
• 对于上图所示 NFA，考虑输入 $abb$，转移过程可以用树状的图来描述，如下图所示

• DFA 和 NFA 是等价的
  • 对于任意 DFA $M$，存在 NFA $M ^ {\prime}$，使得 $L(M)=L(M ^ {\prime})$
  • 对于任意 NFA $M$，存在 DFA $M ^ {\prime}$，使得 $L(M)=L(M ^ {\prime})$
• 证明两者可以相互转化
  • DFA 转化为 NFA 是显然的，DFA 可以直接视作一个特殊的 NFA
  • NFA 转化为 DFA 的思路是：用 DFA 去模拟 NFA 的 tree-like 转移过程，将树的同一层状态整体视作 DFA 的一个状态
• NFA $M=(K, \Sigma, \Delta, s, F)$ 转化为 DFA $M ^ {\prime} = (K ^ {\prime} , \Sigma, \delta, s ^ {\prime} , F ^ {\prime})$
  • $K ^ {\prime} = 2 ^ K = \lbrace Q: Q \sube K \rbrace$
  • $F ^ {\prime} = \lbrace Q \sube K ^ {\prime} : Q \cap F \neq \varnothing \rbrace$
  • $s ^ {\prime} = E(s)$，其中 $E(s)=\lbrace p \in K: (s, e) \vdash _ M (p, e) \rbrace$ 表示 $s$ 通过 $e$-transition 可达的状态集合
  • $\forall Q \in K ^ {\prime}$，$\forall a \in \Sigma$，有 $\delta(Q, a) = \bigcup _ {q \in Q} \bigcup _ {p: (q, a, p)\in \Delta} E(p)$
• 严格证明两者是等价的
  • claim：$\forall p, q \in K$，$\forall w \in \Sigma ^ *$，有 $(p, w) \vdash _ M ^ * (q, e) \Leftrightarrow (E(p), w) \vdash _ {M ^ {\prime}} ^ * (Q, e) \;\text{for some}\; Q \ni q$
  • 先对 $|w|$ 使用数学归纳法证明 claim，再根据自动机接受字符串的定义得证
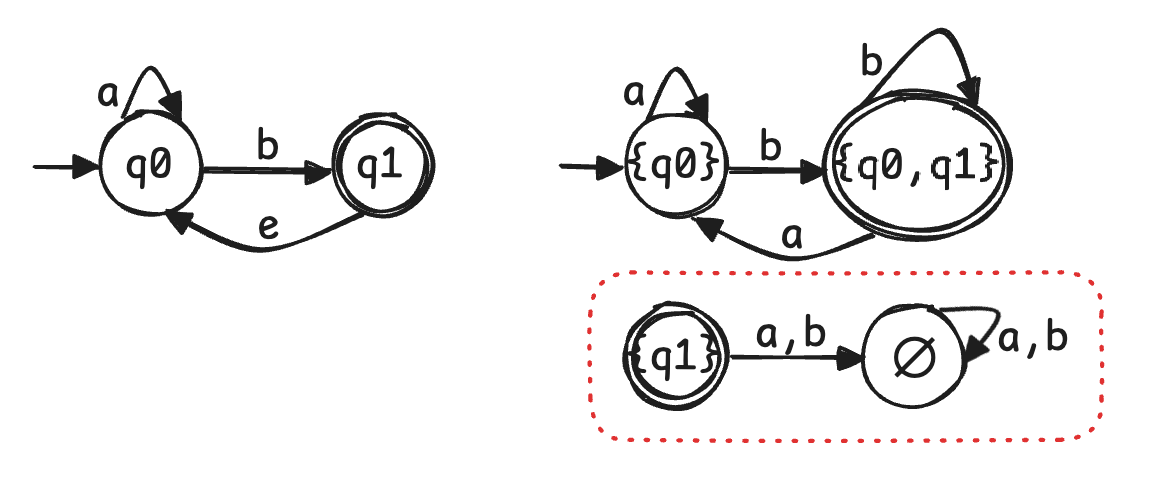
• 下图给出一个 NFA 转化为 DFA 的例子，注意到转化而来的 DFA 下半部分是冗余的，可以舍去
  • 手搓策略：先确定 $s ^ {\prime}$，再从 $s ^ {\prime}$ 出发进行确定性转移，逐步扩展出整个 DFA，这样就不会列出冗余

正则 ¶

正则语言 ¶

• 正则（regular）语言的定义是：能够被某一有限自动机接受的语言
• 正则语言对于下列运算是封闭的，即正则语言的运算结果仍然是正则语言
  • union：$A \cup B = \lbrace w: w\in A \;\text{or}\; w\in B \rbrace$
  • concatenation：$A \circ B = \lbrace ab: a\in A \;\text{and}\; b\in B \rbrace$
  • star：$A ^ * = \lbrace w _ 1 w _ 2 \cdots w _ k : k \geq 0 \;\text{and each}\; w _ i \in A \rbrace$
• 证明正则运算的封闭性
  • union 的思路是并行化，做笛卡尔积
    • $K = K _ A \times K _ B$，$s = (s _ A, s _ B)$，$F = \lbrace (q _ A, q _ B): q _ A \in F _ A \;\text{or}\; q _ B \in F _ B \rbrace$
    • $\forall q _ A \in K _ A$，$\forall q _ B \in K _ B$，$\forall a \in \Sigma$，有 $\delta ((q _ A, q _ B), a) = (\delta (q _ A, a), \delta (q _ B, a))$
  • concatenation 的思路是串行化，用 NFA 的方式来做连接
    • $K = K _ A \cup K _ B$，$s = s _ A$，$F = F _ B$
    • $\Delta = \Delta _ A \cup \Delta _ B \cup \lbrace (q,e,s _ B): q\in F _ A \rbrace$
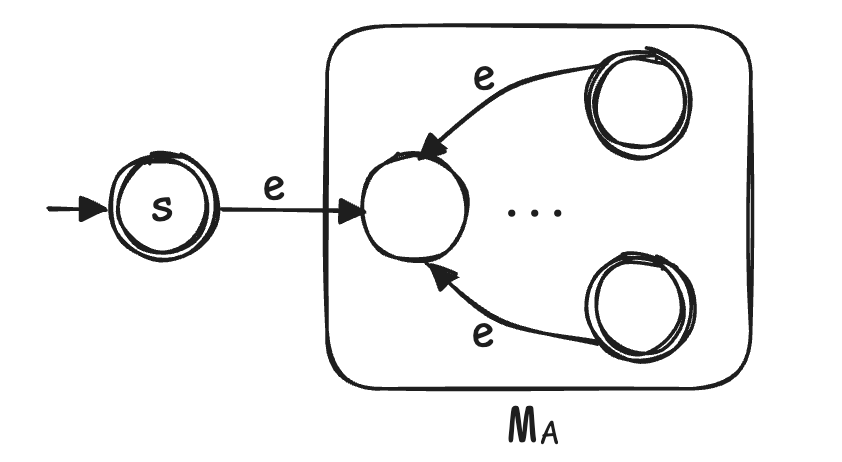
  • star 的思路是循环自身，将终止状态通过 $e$-transition 连接到初始状态，并考虑空串这一特殊情况，如下图所示
    • $K = K _ A \cup \lbrace s \rbrace$，$F = F _ A \cup \lbrace s \rbrace$
    • $\Delta = \Delta _ A \cup \lbrace (s,e,s _ A) \rbrace \cup \lbrace (q,e,s _ A): q\in K _ A \rbrace$

正则表达式 ¶

• 正则表达式由以下规则定义：
  • $\varnothing$ 是一个正则表达式，其对应的语言是 $L(\varnothing) = \varnothing$
  • $a\in \Sigma$ 是一个正则表达式，其对应的语言是 $L(a) = \lbrace a \rbrace$
  • 正则表达式对于下列运算是封闭的，且运算优先级为 $* > \circ > \cup$
    • union：$R _ 1 \cup R _ 2$ 是一个正则表达式，$L(R _ 1 \cup R _ 2) = L(R _ 1) \cup L(R _ 2)$
    • concatenation：$R _ 1 R _ 2$ 是一个正则表达式，$L(R _ 1 R _ 2) = L(R _ 1) \circ L(R _ 2)$
    • star：$R ^ *$ 是一个正则表达式，$L(R ^ *) = (L(R)) ^ *$
• 正则表达式能够描述语言，这是很自然的
  • 例如正则表达式 $\varnothing ^ *$ 描述语言 $\lbrace e \rbrace$
  • 例如正则表达式 $a (a\cup b) ^ * b$ 描述语言 $\lbrace w\in \lbrace a\cup b \rbrace ^ * : w \;\text{starts with}\; a \;\text{and ends with}\; b \rbrace$
• 一个语言是正则语言，等价于其能够被某个正则表达式描述
  • 思路：证明正则表达式与 NFA 的等价性，从而由正则语言的定义得证
• 证明正则表达式与 NFA 的等价性
  • 由正则表达式构建 NFA 是简单的
  • 由 NFA 导出正则表达式的思路是：先简化 NFA，再逐步删除中间状态
• 考虑简化 NFA 以满足以下两个条件，具体方法为改用新的初始 / 终止状态并通过 e-transition 连接
  • 初始状态没有入边
  • 终止状态是唯一的，且没有出边

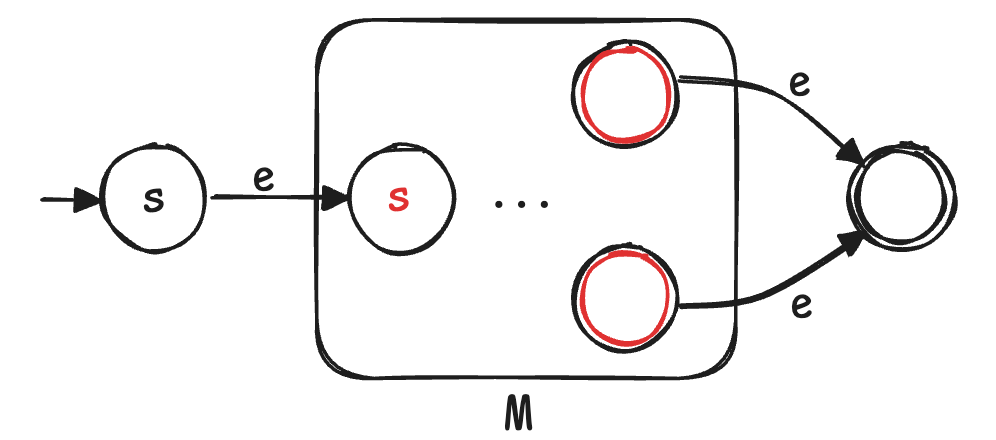
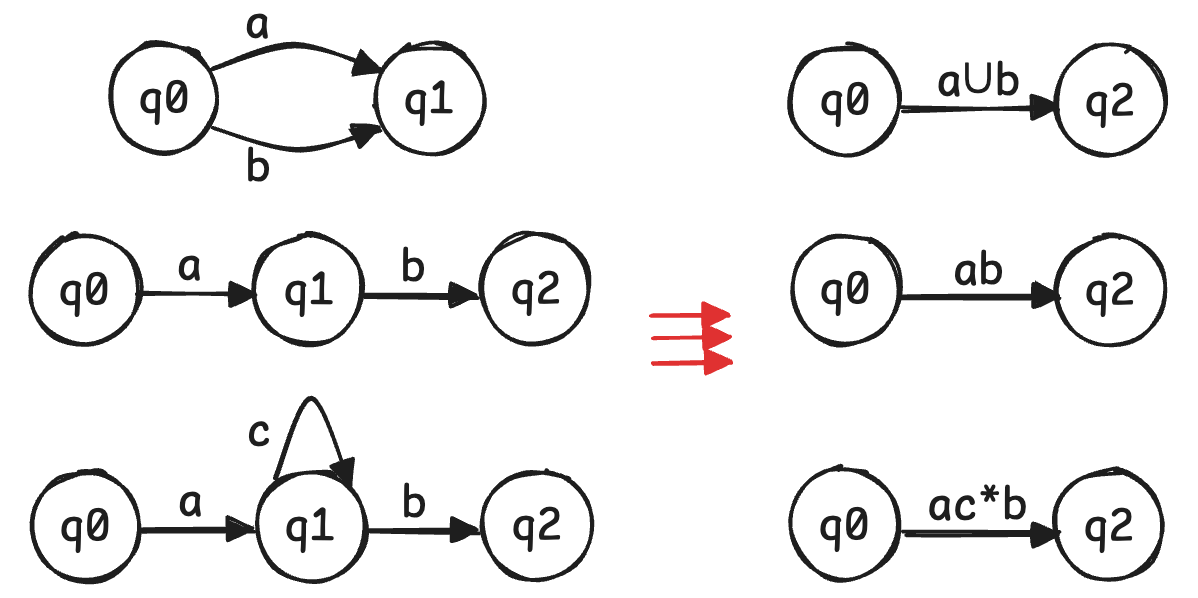
• 考虑删除中间状态，反复使用下图所示方法，不断删除中间状态，直至 NFA 仅由简化的初始状态和终止状态组成，此时转移条件即为导出的正则表达式

• 严格证明由 NFA 导出正则表达式
  • 有 NFA $M=(K, \Sigma, \Delta, s, F)$，其中：
    • $K = \lbrace q _ 1, q _ 2, \cdots, q _ n \rbrace$，$s = q _ {n-1}$，$F = \lbrace q _ n \rbrace$
    • $(p, a, q _ {n-1}) \notin \Delta$，$\forall p\in K$，$\forall a\in \Sigma$
    • $(q _ n, a, p) \notin \Delta$，$\forall p\in K$，$\forall a\in \Sigma$
  • 动态规划
    • 对于 $i, j \in [1,n]$ 以及 $k\in [0,n]$，定义正则表达式 $R _ {ij} ^ k$ 满足 $L _ {ij} ^ k = \lbrace w\in \Sigma ^ * : w \;\text{drives}\; M \;\text{from}\; q _ i \;\text{to}\; q _ j \;\text{with no intermediate state having index}\; > k \rbrace$
    • 目标：求解 $R _ {(n-1)n} ^ {n-2}$，注意到预先完成简化的 NFA 的初始 / 终止状态均不会成为中间状态
    • 已知：可直接写出正则表达式 $R _ {ij} ^ 0$，分 $i=j$ 和 $i\not =j$ 两种情况
    • 递推：由 $R _ {ij} ^ {k-1}$ 推出 $R _ {ij} ^ k$，分为是否经过 $q _ k$ 两种情况，则 $R _ {ij} ^ k = R _ {ij} ^ {k-1} \cup R _ {ik} ^ {k-1} (R _ {kk} ^ {k-1}) ^ {*} R _ {kj} ^ {k-1}$
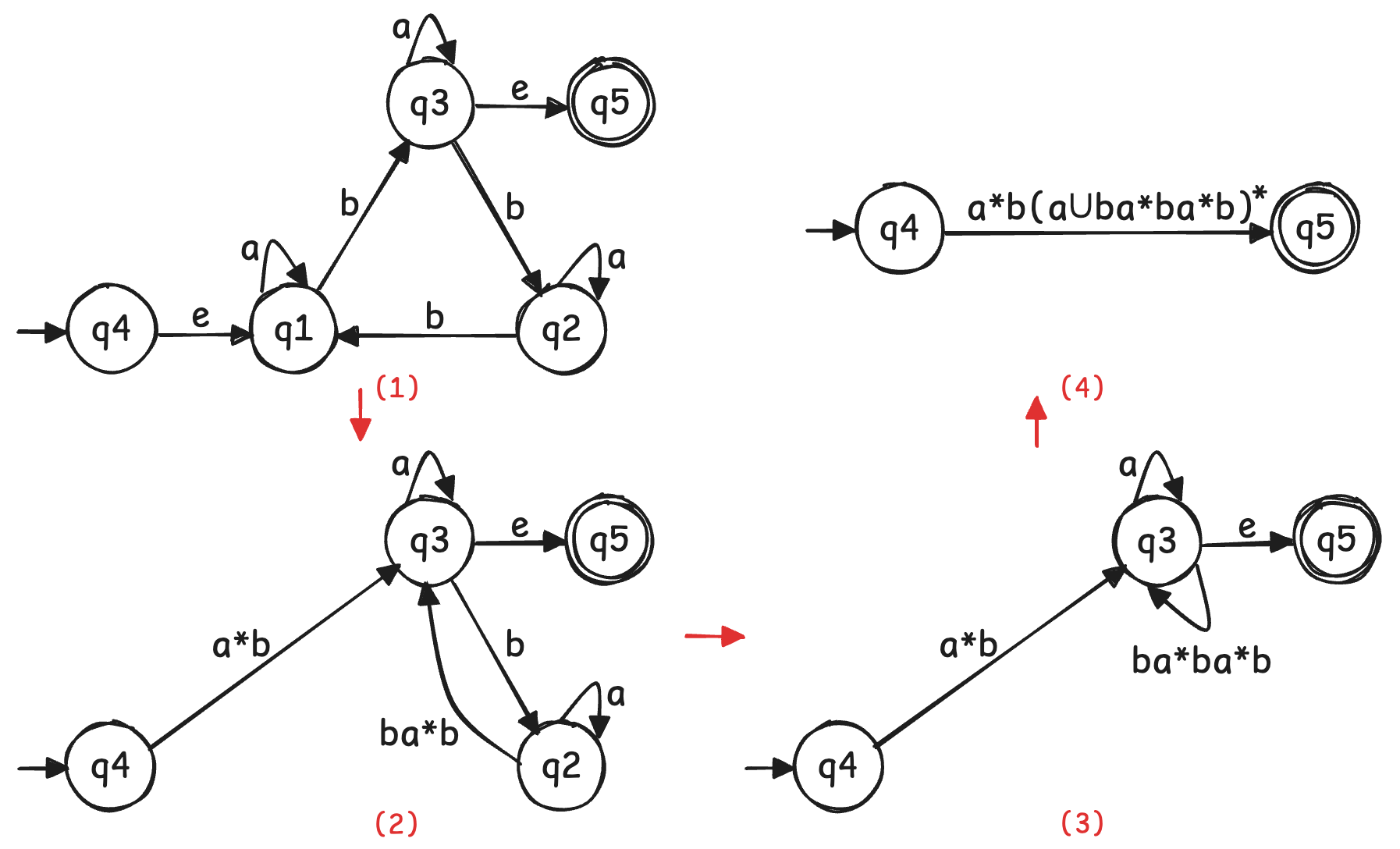
• 下图给出一个由 NFA 导出正则表达式的例子，注意该 NFA 已经预先完成简化

泵定理 ¶

• 设 $L$ 为正则语言，则存在整数 $p \geq 1$（称为 pumping length），使得所有 $|w| \geq p$ 的字符串 $w\in L$ 均可被拆分成三部分 $w=xyz$，且满足：
  • $\forall i\geq 0$，$xy ^ i z \in L$
  • $|y| > 0$
  • $|xy| \leq p$
• 理解 pumping theorem：
  • 对于有限正则语言 $L$，直接取 $p = \max _ {w\in L} |w| + 1$ 即可
  • 对于无限正则语言 $L$，其中充分长的字符串在被相应有限自动机接受的过程中一定存在环
    • 严格证明，考虑 $L$ 对应的 NFA $M$，取 $p=|K|$，长度不小于 $p$ 的字符串一定会经过重复状态（成环），取这个环作为 $y$ 即可
  • pumping theorem 是正则语言的必要条件
• 判定一个语言不是正则的
  • 思路一：反证法，使用 pumping theorem 找矛盾
  • 思路二：反证法，使用 $\cup, \circ, *, \cap, \neg$ 的运算封闭性找矛盾
  • 例如 $L _ 1 =\lbrace 0 ^ n 1 ^ n : n\geq 0 \rbrace$ 不是正则语言，取 $0 ^ p 1 ^ p \in L$ 即可导出矛盾
  • 例如 $L _ 2=\lbrace w\in \lbrace 0, 1 \rbrace ^ {*} : w \;\text{has equal number of}\; 0 \;\text{'s and}\; 1 \;\text{'s} \rbrace$ 不是正则语言，否则根据封闭性 $L _ 1 \cap L _ 2 = L _ 1$ 也是正则语言，导出矛盾