概率论基础 ¶
约 1719 个字 预计阅读时间 7 分钟
概率论的基本概念 ¶
全概率公式与贝叶斯公式 ¶
- 全概率公式是「找结果
」 ,而贝叶斯公式是「找原因」 - 全概率公式解决问题的关键在于如何找到一个合适的「划分」
- 贝叶斯公式中有一些概念值得注意:
- 先验概率:$P(B)$
- 后验概率:$P(B|A)$
- 似然概率:$P(A|B)$
全概率公式与贝叶斯公式
$$ P(A) = \sum_{j=1}^n{P(B_j) P(A|B_j)} $$
$$ P(B_i|A) = \frac{P(AB_i)}{P(A)} = \frac{P(B_i) P(A|B_i)}{\sum_{j=1}^n{P(B_j) P(A|B_j)}} $$
随机变量及其概率分布 ¶
随机变量补充 ¶
- 离散型和连续型是常见的两类随机变量,但随机变量并不只有这两种。
- 书写离散型随机变量的概率分布律时千万不要漏掉随机变量的可能取值。例如:$k=1,2,...$
分布函数补充 ¶
- 分布函数通常写成大写字母,例如 $F(x)$
- 分布函数的定义域为全体实数
- 分布函数的分段写法,按照「左闭右开」的区间进行分段是一个较好的习惯(主要针对离散型随机变量的分布函数)
- 支撑(support)指的是使概率分布为正的密度的随机变量的取值的集合,定义为 $ \lbrace x: f(x)>0\rbrace $
概率密度函数理解 ¶
有一个常见的误区,就是错把连续型随机变量的「概率密度函数的函数值」和连续型随机变量的「概率」直接划等号。事实上,概率密度函数的函数值代表的是概率分布函数的变化率(所以概率密度函数的函数值大于 $1$ 也是很合理的
那么,概率密度函数和概率的联系到底是什么呢?结论是,某段区间上「概率密度函数的面积(积分
关于概率密度函数,我们有更加直观的解释。概率密度函数的函数值较大的地方,代表这个点附近的概率「密度」较大,也就是说随机变量落在这个点附近的单位长度区间上的概率较大。用数学公式表示就是 $f(x) \Delta x = P = \Delta F(x)$。
指数分布的无记忆性 ¶
假设 $t_0>0$,$t>0$,
$$ \begin{aligned} P(X>t_0+t \;\; | \;\; X>t_0 ) & = \frac{P(X>t_0+t)}{P(X>t_0)} \cr & = \frac{1-F(t_0+t)}{1-F(t_0)} \cr & = e^{-\lambda t} = P(X>t) \end{aligned} $$
$$ \begin{aligned} P(X\lt t_0+t \;\; | \;\; X>t_0) & = \frac{P(t_0\lt X\lt t_0+t)}{P(X>t_0)} \cr & = \frac{F(t_0+t)-F(t_0)}{1-F(t_0)} \cr & = 1-e^{-\lambda t} = P(X<t) \end{aligned} $$
无记忆性的一个例子
假设设备无故障运行的时间 $T$ 服从指数分布。已知设备无故障运行了 10 个小时,求该设备再无故障至少运行 8 个小时的概率。
$$ P\lbrace T\geq 18 \; | \; T>10 \rbrace = \frac{P\lbrace T>18\rbrace }{P\lbrace T>10\rbrace} = e^{-8\lambda} = P\lbrace T>8\rbrace $$
注意到,这一条件概率与无条件下无故障运行 8 小时的概率没有区别。
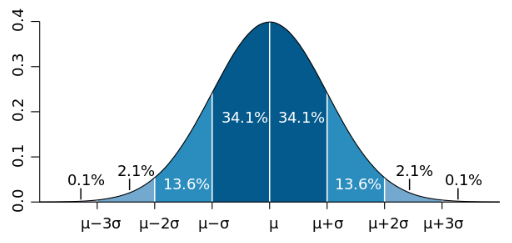
正态分布标准化 ¶
当 $X\sim N(\mu,\sigma^2)$ 时:
$$ P(X\leq b) = \int_{-\infty}^b \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu) ^2}{2\sigma ^2}} \mathrm{d}x $$
做变换:$\frac{x-\mu}{\sigma} = t$
$$ \begin{aligned} P(X\leq b) & = \int_{-\infty}^{\frac{b-\mu}{\sigma}} \frac{1}{\sqrt{2\pi}} e^{-\frac{t ^2}{2}} \mathrm{d}t \cr & = \Phi(\frac{b-\mu}{\sigma}) \end{aligned} $$
换言之,当 $X\sim N(\mu,\sigma^2)$ 时,$\frac{X-\mu}{\sigma}\sim N(0,1)$
随机变量的函数分布 ¶
一般地,若已知 $X$ 的概率分布,$Y=g(X)$,求 $Y$ 的概率分布的思路为:先给出 $Y$ 的可能取值,再利用「等价事件」求解 $Y$ 的概率分布函数或概率密度函数。
- 对于离散型随机变量,比较简单,在此不赘述;
- 对于连续型随机变量,可以按照以下步骤求解:
- 写出 $Y$ 的概率分布函数 $F_Y(y)=P(Y \leq y)$;
- 找出 $(Y \leq y)$ 的等价事件 $(X \in D)$,得到 $F_Y(y)=P(X \in D)$,解出 $Y$ 的概率分布函数;
- 进而求解 $Y$ 的概率密度函数 $f_Y(y) = \frac{\mathrm{d}}{\mathrm{d}y} F_Y(y)$;
特别地,若解出概率分布函数为 $F_Y(y) = F_X(h(y))$,则概率密度函数也可写成 $f_Y(y) = \frac{\mathrm{d}}{\mathrm{d}(h(y))} F_X(h(y)) \cdot \frac{\mathrm{d}(h(y))}{\mathrm{d}y} = f_X(h(y)) \cdot h^{\prime}(y)$;
多元随机变量及其分布 ¶
二维离散型随机变量补充 ¶
对于任何分布律都有两条性质(对联合、边际、条件分布律都成立
- $p_{ij} \geq 0, \; i,j=1,2,\dots$
- $\sum_{i=1}^{\infty} \sum_{j=1}^{\infty} P_{ij} = 1$
二维随机变量的分布函数补充 ¶
- 联合分布函数 $F(x,y) = P(X \leq x, Y \leq y)$ 是二元函数
- 边际分布函数 $F_X(x) = P(X \leq x) = lim_{y \rarr +\infty}F(x,y)$ 是关于 $x$ 的一元函数
- 条件分布函数 $F_{X \mid Y}(x \mid y) = P(X \leq x \mid Y=y)$ 是关于 $x$ 的一元函数
- $\lim_{\epsilon \rarr 0^+}P(X\leq x\mid y<Y\leq y+\epsilon)$ 也记为 $P(X \leq x \mid Y=y)$,请特别注意这个记号所带来的两种理解
联合分布、边际分布、条件分布满足如下关系:
二维连续型随机变量补充 ¶
- 条件密度函数的重要性质:
- $f(x,y) = f_{X|Y}(x|y)f_Y(y) = f_{Y|X}(y|x)f_X(x)$
- 直观意义:
$f_{X|Y}(x \mid y) \Delta x = \frac{f(x,y)\Delta x \Delta y}{f_Y(y)\Delta y} \approx \frac{P(x<X\leq x+\Delta x, \; y<Y\leq y+\Delta y)}{P(y<Y\leq y+\Delta y)} = P(x<X\leq x+\Delta x \mid y<Y\leq y+\Delta y)$
- 二维均匀分布的条件分布为一维均匀分布
- 二维正态分布的边际分布和条件分布为一维正态分布(不依赖于 $\rho$)
- 二维正态分布的记号:$(X,Y) \sim N({\mu}_1, \; {\mu_2}; \; {\sigma}_1^2, \; {\sigma}_2^2; \; \rho)$
随机变量的独立性补充 ¶
- 若 $(X,Y)$ 是离散型随机变量,则 $X,Y$ 相互独立等价于 $p_{ij} = p_{i\cdot}p_{\cdot j}$ 对一切 $i,j$ 都成立
- 若 $(X,Y)$ 是连续型随机变量,则 $X,Y$ 相互独立等价于 $f(x,y) = f_X(x)f_Y(y)$ 总是成立,平面上“面积”为零的集合除外(可以在不连续点上不相等)
- 此外,$X,Y$ 相互独立也等价于存在一元函数 $m,n$,使得 $f(x,y)=m(x)n(y)\;,\;|x|<+\infty,|y|<-\infty$(注意:联合密度函数的函数式和定义域均须可分)
- 二维正态分布是独立的,等价于 $\rho = 0$
- $n$ 维随机变量独立性相关定理:
- 设 $(X_1,X_2,\cdots ,X_m)$ 与 $(Y_1,Y_2,\cdots ,Y_n)$ 相互独立,则 $X_i(i=1,2,\cdots ,m)$ 与 $Y_j(j=1,2,\cdots ,n)$ 相互独立
- 设 $(X_1,X_2,\cdots ,X_m)$ 与 $(Y_1,Y_2,\cdots ,Y_n)$ 相互独立,若 $h(x_1,x_2,\cdots ,x_m)$ 与 $g(y_1,y_2,\cdots ,y_n)$ 是连续函数,则 $h(X_1,X_2,\cdots ,X_m)$ 与 $g(Y_1,Y_2,\cdots ,Y_n)$ 相互独立
二维随机变量的函数分布 ¶
- $Z=X+Y$ 的分布(这里讨论连续型,离散型只需把积分符号换成求和符号即可)
- $f_Z(z)=\int_{-\infty}^{+\infty}f(z-y,y)\mathrm{d}y=\int_{-\infty} ^ {+\infty}f(x,z-x)\mathrm{d}x$($x$,$y$ 是对称的)
- 当 $X$ 和 $Y$ 相互独立时,$Z$ 的密度函数公式也称为卷积公式:$f_X*f_Y=\int_{-\infty}^{+\infty}f_X(z-y)f_Y(y)\mathrm{d}y=\int_{-\infty} ^ {+\infty}f_X(x)f_Y(z-x)\mathrm{d}x$
- $M=max(X,Y)$ 与 $N=min(X,Y)$ 的分布(基于 $X$ 和 $Y$ 相互独立)
- $F_{max}(z)=F_X(z)F_Y(z)$
- $F_{min}(z)=1-(1-F_X(z))(1-F_Y(z))$
- $n$ 个相互独立的随机变量同理
常见分布的卷积 ¶
分布的卷积问题,也即是分布的独立可加性问题。
1. 二项分布的可加性:设 $X\sim B(n,p)$,$Y\sim B(m,p)$,$0<p<1$,$m$,$n$ 均为正整数,若 $X$ 与 $Y$ 独立,则
$$ X+Y\sim B(m+n,p) $$
二项分布的可加性有助于理解二项分布与两点分布的可加性。
2. 泊松分布的可加性:设 $X\sim P({\lambda}_1)$,$Y\sim P({\lambda}_2)$,${\lambda}_i>0$,$i=1,2$,若 $X$ 与 $Y$ 独立,则
$$ X+Y\sim P({\lambda}_1+{\lambda}_2) $$
3. 正态分布的可加性:设 $X\sim N({\mu}_1,{\sigma}_1^2)$,$Y\sim N({\mu}_2,{\sigma}_2^2)$,$-\infty <{\mu}_i<+\infty$,${\sigma}_i>0$,$i=1,2$,若 $X$ 与 $Y$ 独立,则
$$ X+Y\sim N({\mu}_1+{\mu}_2,{\sigma}_1^2+{\sigma}_2 ^ 2) $$
此外,若 $(X,Y)\sim N({\mu}_1,{\mu}_2,{\sigma}_1^2 ,{\sigma}_2^2 ,\rho)$,则不论 $X$ 与 $Y$ 是否独立(即 $\rho$ 是否为 $0$
$$ aX+bY+c\sim N(a{\mu}_1+b{\mu}_2+c,a^2 {\sigma}_1^2 +b^2 {\sigma}_2 ^ 2 + 2ab{\sigma}_1{\sigma}_2\rho) $$
4.$\Gamma$ 分布的可加性:设 $X\sim \Gamma ({\alpha}_1,\beta)$,$Y\sim \Gamma ({\alpha}_2,\beta)$,${\alpha}_i>0$,$i=1,2$,$\beta >0$ 均为正整数,若 $X$ 与 $Y$ 独立,则
$$ X+Y\sim \Gamma ({\alpha}_1+{\alpha}_2,\beta) $$
指数分布是特殊的 $\Gamma$ 分布,$E(\lambda)=\Gamma (1,\lambda)$。
随机变量的数学特征 ¶
常见分布的期望与方差 ¶
| 分布 | 分布律或密度函数 | 数学期望 | 方差 |
|---|---|---|---|
| $0-1$ 分布 | $P(X=k)=p^k (1-p)^{1-k},\;\;k=0,1$ | $p$ | $p(1-p)$ |
| 二项分布 $B(n,p)$ | $P(X=k)=C_n^k p^k (1-p)^{1-k},\;\;k=0,1,...,n$ | $np$ | $np(1-p)$ |
| 泊松分布 $P(\lambda)$ | $P(X=k)=\frac{\lambda ^k e^{-\lambda}}{k!},\;\;k=0,1,...$ | $\lambda$ | $\lambda$ |
| 均匀分布 $U(a,b)$ | $f(x)=\begin{cases} \frac{1}{b-a} & ,a<x<b \cr 0 & ,\text{else} \end{cases}$ | $\frac{a+b}{2}$ | $\frac{(b-a)^2}{12}$ |
| 指数分布 $E(\lambda)$ | $f(x)=\begin{cases} \lambda e^{-\lambda x} & ,x>0 \cr 0 & ,\text{else} \end{cases}$ | $\frac{1}{\lambda}$ | $\frac{1}{\lambda ^2}$ |
| 正态分布 $N(\mu ,\sigma ^2)$ | $f(x)=\frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu) ^2 }{2\sigma ^2 }},\;\;-\infty<x<+\infty$ | $\mu$ | $\sigma ^2$ |
数学期望与分布函数的关系 ¶
设随机变量 $X$ 的分布函数为 $F(x)$,则分部积分法易证:
$$ E(X) = \int_{0}^{+\infty} (1-F(x))\mathrm{d}x-\int_{-\infty}^{0} F(x)\mathrm{d}x $$
- 当 $X$ 为非负随机变量(即 $P(X\geq 0)=1$)时,有:$E(X)=\int _0^{+\infty} (1-F(x))\mathrm{d}x$;
- 当 $X$ 为取非负整数值得随机变量时,有:$E(X)=\sum _{k=1}^{+\infty} P(X\geq k)$;
二维随机变量函数的数学期望 ¶
设 $Z$ 是随机变量 $X,Y$ 的函数:$Z=h(X,Y)$($h$ 是连续函数
- 若二维离散型随机变量 $(X,Y)$ 的分布律为 $P(X=x_i,Y=y_j)=p_{ij},\;\;i,j=1,2,...$,则有:$E(Z)=E[h(X,Y)]=\sum_{i=1}^{\infty} \sum_{i=1}^{\infty} h(x_i,y_j)p_{ij}$,这里设上式右边的级数绝对收敛;
- 若二维连续型随机变量 $(X,Y)$ 的概率密度为 $f(x,y)$,则有:$E(Z)=E[h(X,Y)]=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} h(x,y)f(x,y)\mathrm{d}x\mathrm{d}y$,这里设上式右边的积分绝对收敛;
- 特别地:
- $E(XY)=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} xyf(x,y)\mathrm{d}x\mathrm{d}y$;
- $E(X)=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} xf(x,y)\mathrm{d}x\mathrm{d}y$;
- $E(Y)=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} yf(x,y)\mathrm{d}x\mathrm{d}y$;
条件数学期望 ¶
若 $(X,Y)$ 为二维离散型随机变量,且在给定 $X=x$ 下,$Y$ 的条件分布律为 $P(Y=y_j | X=x)=p_j(x),\;\;j=1,2,...$;或者 $(X,Y)$ 为二维连续型随机变量,且在给定 $X=x$ 下,$Y$ 的条件概率密度函数为 $f_{Y|X}(y|x)$,则 $Y$ 的条件期望为:
$$ E(Y|X=x)= \begin{cases} \sum_{j=1}^{+\infty} y_j p_j(x) & ,\text{discrete} \cr \int_{-\infty}^{+\infty} y f_{Y|X}(y|x) \mathrm{d}y & ,\text{continuous} \end{cases} $$
$(X,Y)$ 为二维随机变量,若 $E(Y)$ 存在,则有全期望公式(Total Expectation Formula
$$ E(Y) = E[E(Y|X)] $$
标准化变量 ¶
设随机变量 $X$ 具有数学期望 $E(X)=\mu$,方差 $D(X)=\sigma ^2 \neq 0$,记 $X^{*} = \frac{X-\mu}{\sigma}$。$E(X^{*} )=0$,$D(X^{*})=1$,称 $X^{*}$ 为 $X$ 的标准化变量。
特别地,正态变量的标准化变量服从标准正态分布。
独立性与相关性 ¶
随机变量之间的相关性仅针对「线性关系」而言,$X,Y$ 不相关等价于 $Cov(X,Y)=0$。
而独立性是一个很强的条件,随机变量相互独立,定义上要求其中任一变量的存在与否,都不会对其他变量的概率分布产生影响。$X,Y$ 独立等价于 $Cov(f(X),g(Y))=0$ 对任何函数 $f,g$ 都成立,也就是说要求 $X,Y$ 没有任何关系,包括线性的和非线性的。
所以我们发现,独立性比相关性强得多,独立是不相关的充分不必要条件。通俗地讲,独立才是我们所说的“没有关系”,而不相关仅仅表达“没有线性关系”。
二维正态变量 $(X,Y)$ 的独立性与相关性:
- $\rho _{XY} = \rho$;
- $X,Y$ 相互独立 $\Rightarrow$ $X,Y$ 不相关;
其它数字特征 ¶
设 $X,Y$ 是随机变量:
- 若 $E(X^k),\;\;k=1,2,...$ 存在,则称之为 $X$ 的 $k$ 阶(原点)矩;
- 若 $E\lbrace [X-E(X)]^k \rbrace,\;\;k=1,2,...$ 存在,则称之为 $X$ 的 $k$ 阶中心矩;
- 若 $E(X^k Y^l),\;\;k,l=1,2,...$ 存在,则称之为 $X,Y$ 的 $k+l$ 阶混合(原点)矩;
- 若 $E\lbrace [X-E(X)]^k [Y-E(Y)]^l \rbrace,\;\;k,l=1,2,...$ 存在,则称之为 $X,Y$ 的 $k+l$ 阶混合中心矩;
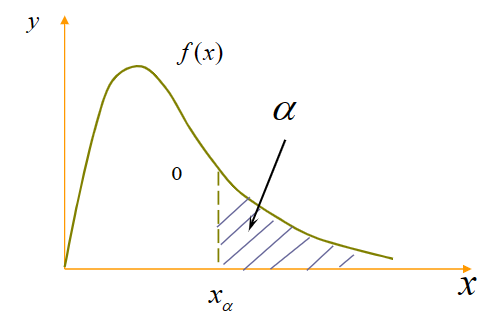
设 $X$ 为连续型随机变量,其分布函数和概率密度函数分别为 $F(x)$ 和 $f(x)$,称满足条件 $P(X>x_{\alpha})=1-F(x_{\alpha})=\int_{x_{\alpha}}^{+\infty} f(x) \mathrm{d}x = \alpha$ 的实数 $x_{\alpha}$ 为随机变量 $X$ 的上 $x_{\alpha}$ 分位数。
- 当 $\alpha = ½$ 时,$x_{½}$ 称为 $X$ 的中位数;
- 对于标准正态分布,$x_{½}=0$,$x_{1-\alpha}=-x_{\alpha}$;
创建日期: 2024年2月8日 16:17:32