时序逻辑设计 ¶
约 1976 个字 预计阅读时间 8 分钟
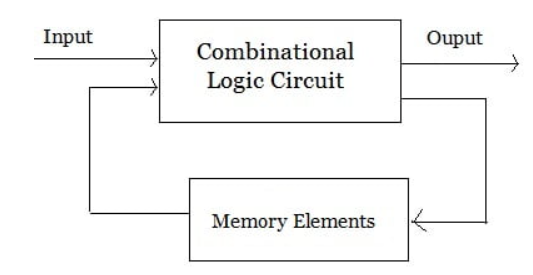
时序逻辑理解 ¶
以下是 Wikipedia 对于时序逻辑、同步与异步的定义:
Sequential logic is a type of logic circuit whose output depends on the present value of its input signals and on the sequence of past inputs.
That is, sequential logic has state (memory) while combinational logic does not.Digital sequential logic circuits are divided into synchronous and asynchronous types.
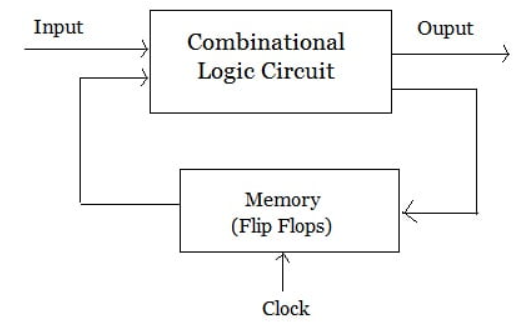
In synchronous sequential circuits, the state of the device changes only at discrete times in response to a clock signal.
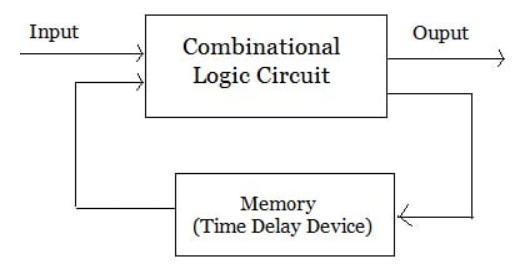
In asynchronous circuits the state of the device can change at any time in response to changing inputs.
很自然地,异步时序逻辑是 input-driven 的,每当输入发生变化,就要进行状态的更新。但是,异步时序逻辑的弊端在于,当输入包含多个变量而它们的抵达有先后区分的时候,电路可能会偏离预期而进入错误的状态。
同步时序逻辑可以解决这个问题。我们使用一个时钟信号来同步(synchronize, or clock)所有输入变量产生作用的时间,即使输入变量先后抵达,它们也得等待时钟信号来临时才能发生作用,从而更新电路的状态。
工程应用中,同步时序逻辑往往更为普遍,因为其设计简单而且鲁棒性强。异步时序逻辑的设计通常更为复杂,多用于需要更高更新速度的场合(不像同步时序逻辑那样受限于时钟信号的频率
从锁存器到触发器 ¶
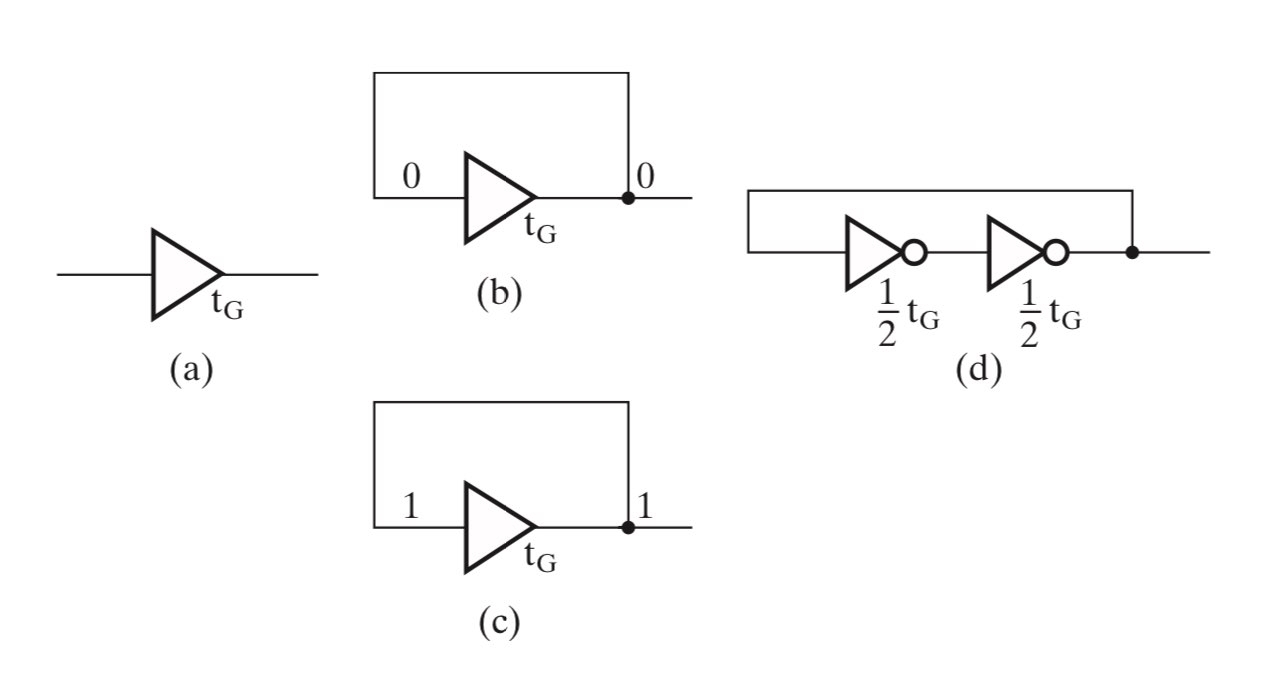
某种意义上,延迟可以用于实现信息存储。对于一个存在 $t_G$ 延迟的 buffer 而言,我们可以认为信息在 $t_G$ 这段时间内是不变的,即被短暂地存储了(如图 a
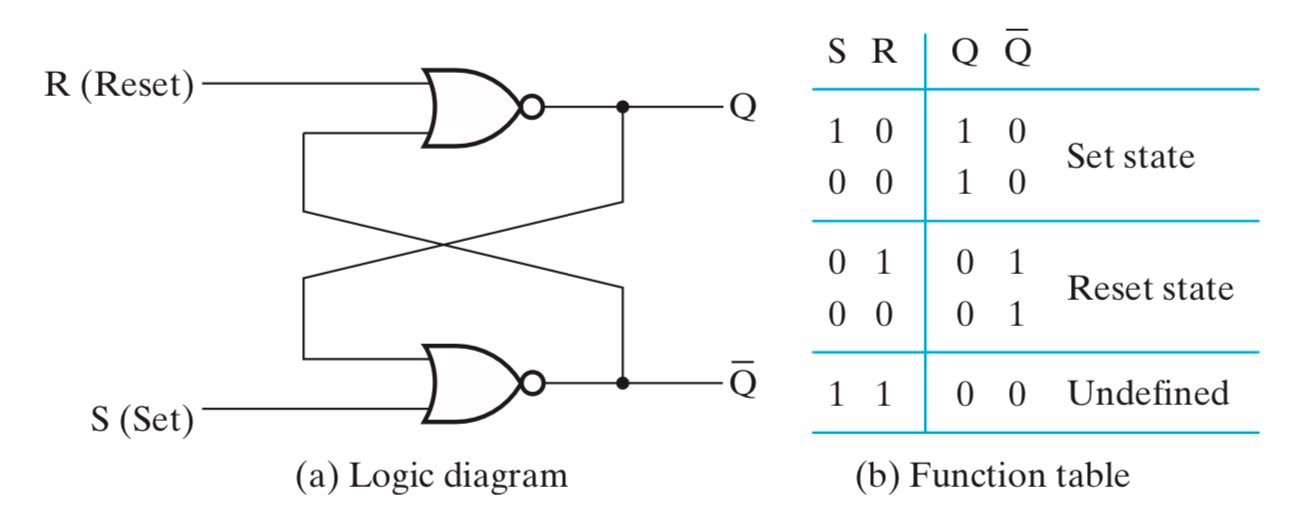
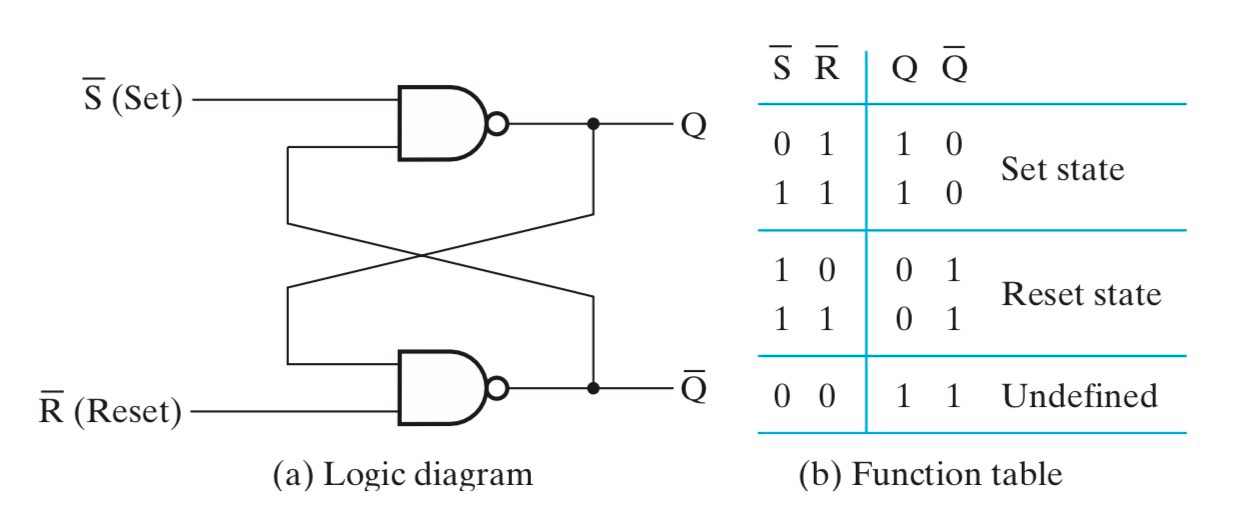
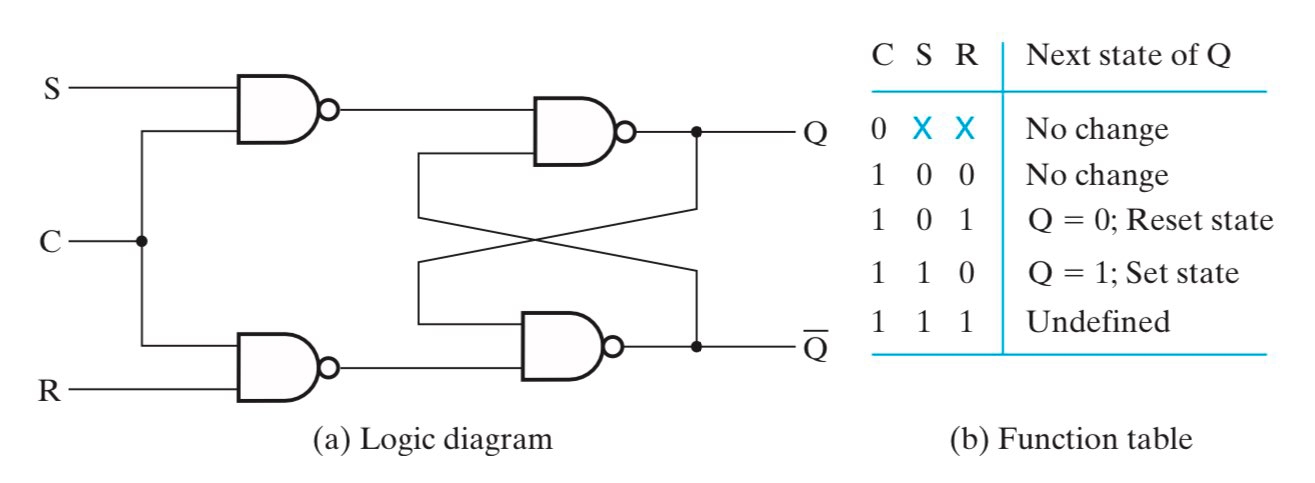
我们把组成 buffer 的非门(如图 d)替换成或非门或者与非门,就可以方便地修改存储的信息内容,这就是 $SR$ Latch。稍加思考不难发现,这样的一个 $SR$ Latch 其实是异步的,因而输入 S 和 R 的先后抵达可能导致电路偏离预期而进入错误的状态。我们可以通过增加一个使能控制端 C 来确保 S 和 R 都到位时再使能,这就是 $SR$ Latch with Control Input(注意这并不是严格意义上的同步,当 C 置1时其仍然是异步的1。
对于 $SR$ Latch with Control Input 而言,用 S 和 R 均置0来表示保持态是多余的(因为 C 置0即可表示保持态
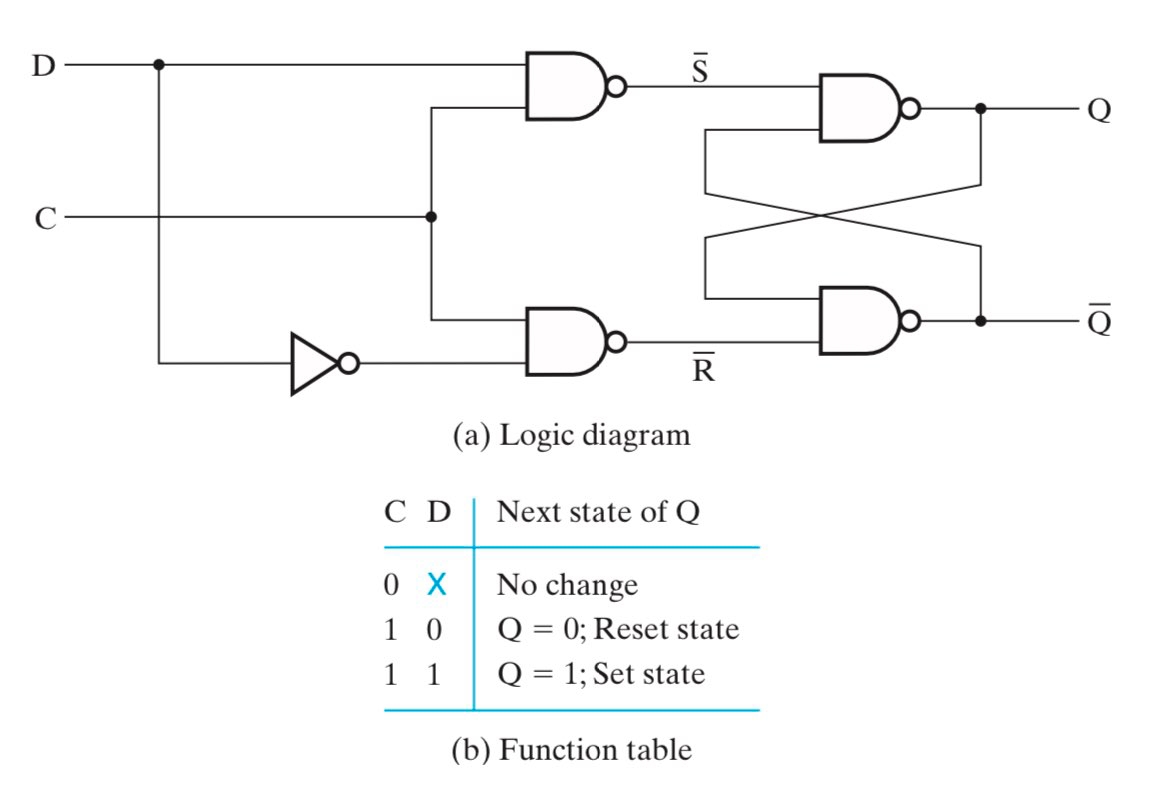
总结一下,我们从 buffer 出发,逐步解决信息存储和修改的问题,最终设计出了 $D$ Latch。然而,$D$ Latch 也并不是完美的。事实上,$D$ Latch 存在的问题,也是所有的 Latch 都无法规避的问题,即透明(transparent, which means its input value can be seen from the outputs while the control input is 1
透明为什么会产生问题呢?在时序逻辑电路中,总是存在从信息存储单元到组合逻辑电路的反馈路径,因此对于一个 Latch 而言,其输入总是部分来自自身或其他 Latch 的输出。由于 Latch 是透明的,在同一个时钟周期内,输出可能会反过来修改输入,从而导致 Latch 的状态更新发生了不止一次。这个问题是很严重的,对于透明的 Latch 而言,一个时钟周期内状态更新的次数,取决于时钟周期的长短和反馈路径的组合电路延迟,导致我们无法确定这个时钟周期结束后 Latch 究竟处在什么状态。
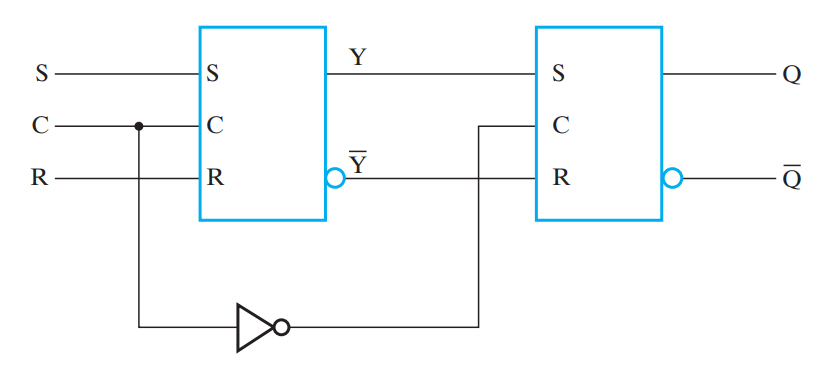
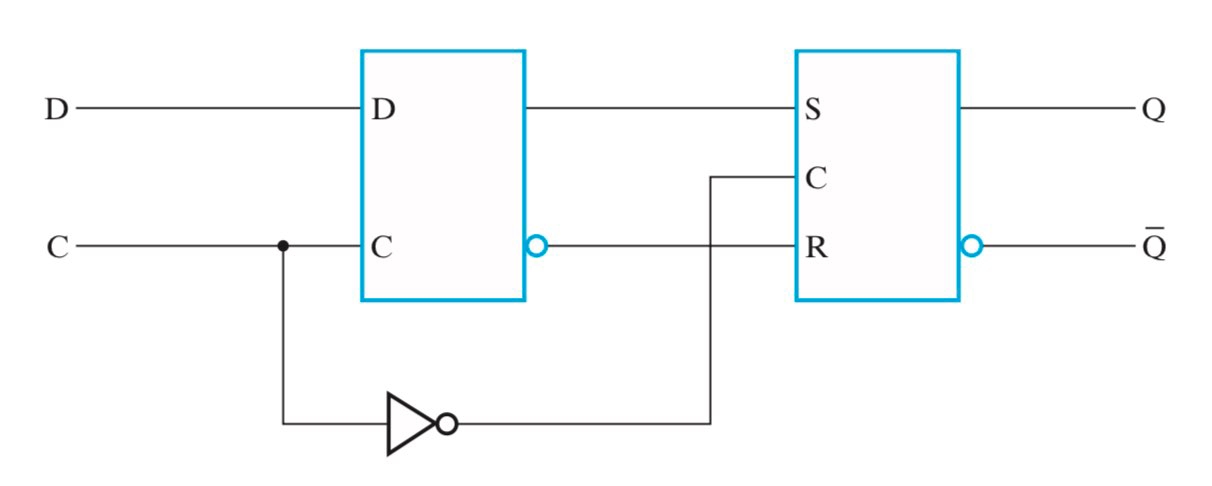
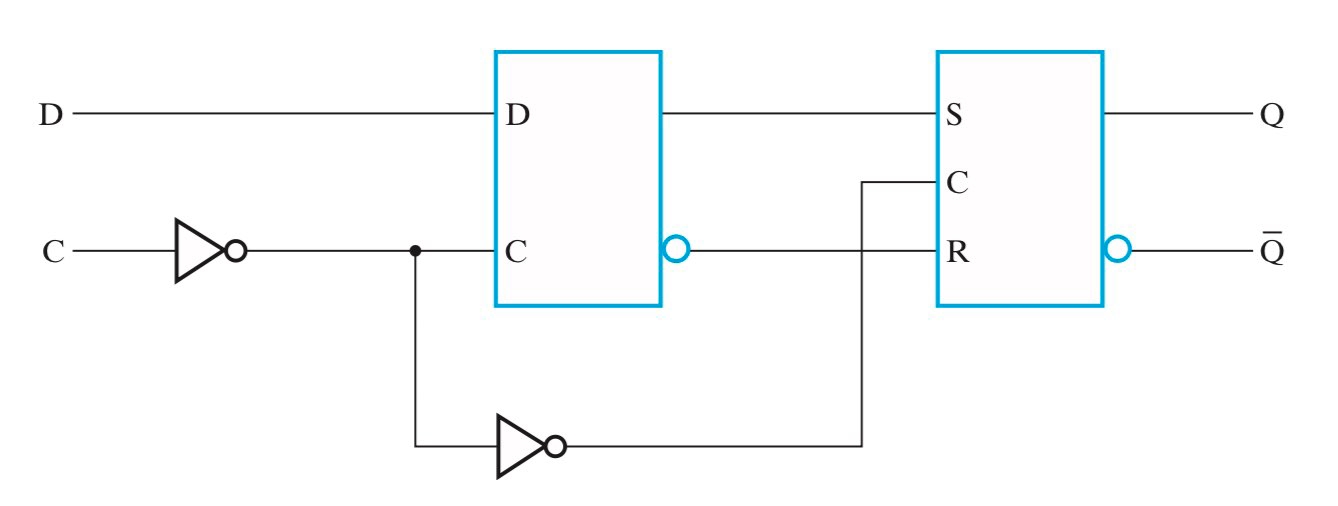
上文提到,Latch 是透明的,所以无法确定一个时钟周期内状态更新的次数。我们希望设计一个非透明的信息存储单元,确保一个时钟周期内仅发生一次状态更新。通常的解决方法是,把两个 Latch 串联起来,当时钟信号为1时,主 Latch 写入,从 Latch 只读;当时钟信号为0时,主 Latch 只读,从 Latch 写入。因此,在一个时钟周期内,前一半时间更新主 Latch,后一半时间更新从 Latch,从而对于整体而言,仅发生一次状态更新,这就是主从触发器(Master-Slave Flip-Flop
教材中的传统观点
Logic and Computer Design Fundamentals 教材中认为,主从触发器有两种实现方法:pulse-triggered 和 edge-triggered。
$SR$ 触发器就属于前者。但是,$SR$ 触发器存在一个很大的问题,即 1s-catching。当时钟信号为1时,S 或 R 短暂的置1均会被 Master 捕捉到,并在时钟信号为0时传递给从 Slave。由于时序逻辑电路总是存在反馈路径,所以同一个时钟周期内 Master 的状态可能会更新多次,虽然对于触发器整体而言仍然仅有一次状态更新(因为 Slave 仅更新一次
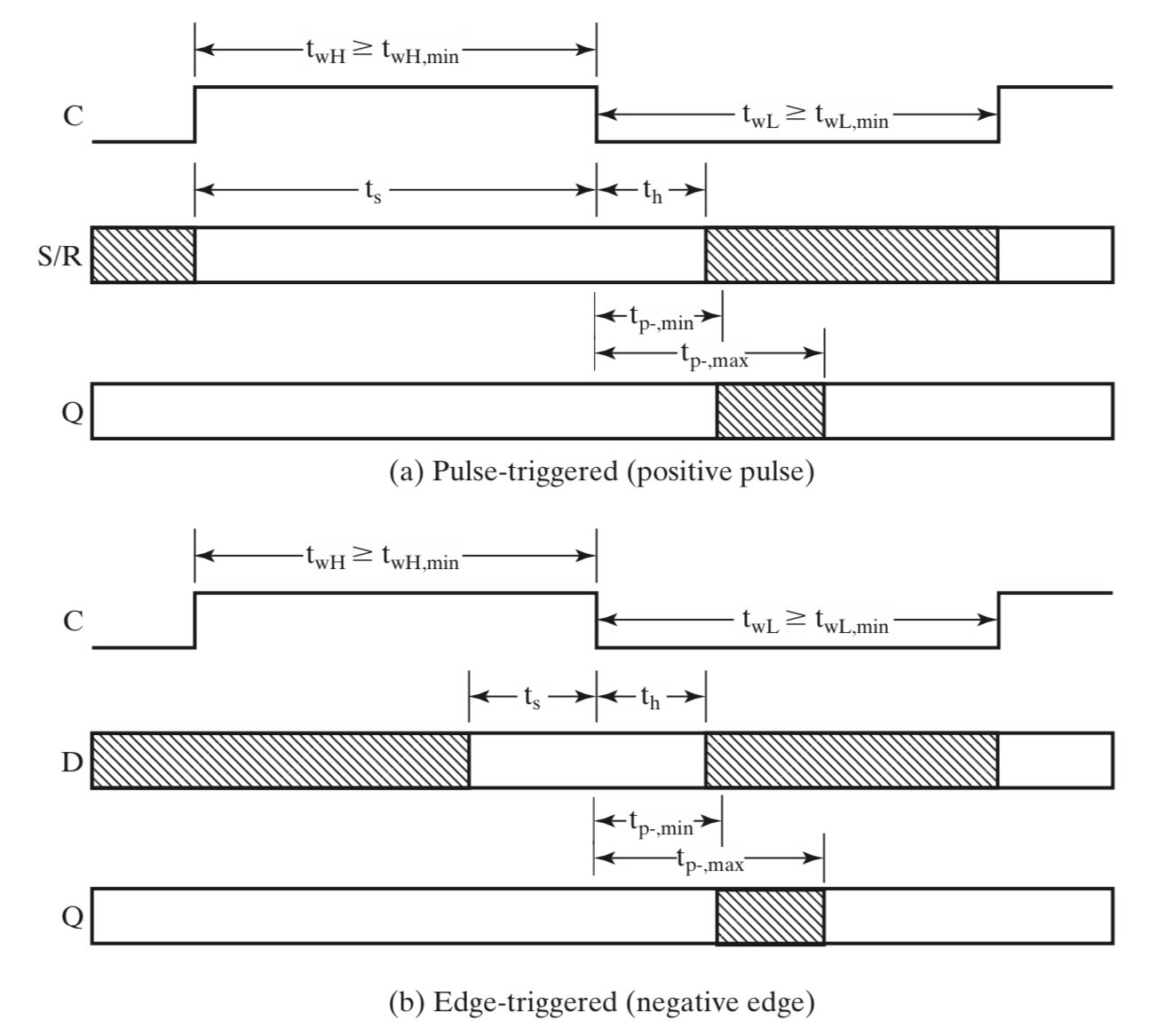
为了更好地理解 1s-catching,让我们回忆一下时序逻辑延迟分析中提到的 setup-time(如下图1时触发器输入端总是稳定的,从而确保不会发生 1s-catching。
更进一步地,1s-catching 可以被认为是亚稳态(metastability)的一种表现。当我们没能在 setup-time 期间维持数据稳定,就会导致触发器陷入亚稳态。通常的解决思路是串联两层甚至更多层的触发器。
读到这里,或许你也和笔者一样,产生了如下的疑惑:
为什么我感觉 pulse-triggered 和 1s-catching 的概念更像是 Latch 的特性?
如果我把注意力集中在时钟信号边沿,难道 pulse-triggered 不也具有 edge-triggered 特性吗?
难道 pulse-triggered flip-flop 不是伪命题吗?
现代观点认为,触发器并不存在所谓的 pulse-triggered(or level-triggered)类型。正如马德老师在课堂上一再强调的,真正存在实用价值的是边沿触发式(edge-triggered)触发器,比如广泛使用的 $D$ 触发器。严格来说,在数字逻辑设计这门课中,我们所说的 $D$ 触发器其实是边沿触发式 $D$ 主从触发器(Master-Slave Edge-Triggered $D$ Flip-Flop
以下是 Wikipedia 对于触发器的描述:
The term flip-flop has historically referred generically to both level-triggered (asynchronous, transparent, or opaque) and edge-triggered (synchronous, or clocked) circuits that store a single bit of data using gates.
Modern authors reserve the term flip-flop exclusively for edge-triggered storage elements and latches for level-triggered ones.
总结一下:
- Latch 是异步的、透明的、脉冲触发的,在整个时钟信号为
1的过程中均可写入信息并多次更新状态; - Flip-Flop 是同步的、非透明的、边沿触发的,一个时钟周期内仅在时钟信号的上升沿或下降沿进行一次状态的更新;
除此以外,还有很多种其他的触发器设计,比如数逻课堂上提到的 $T$ Flip-Flop 和 $JK$ Flip-Flop,更多相关知识可以参考 https://en.wikipedia.org/wiki/Flip-flop_(electronics)。
创建日期: 2024年2月8日 16:17:32