数字逻辑基础 ¶
约 1643 个字 预计阅读时间 7 分钟
数字系统与编码 ¶
基本概念 ¶
两种逻辑系统:
- 组合逻辑(Combinational Logic
) :任意时刻的输出仅取决于该时刻的输入 - 时序逻辑(Suquential Logic
) :任意时刻的输出既取决于该时刻的输入,也取决于电路原来的状态- 同步(Synchronous
) :State updated at discrete times - 异步(Asynchronous
) :State updated at any time
- 同步(Synchronous
数字系统与编码的概念是不一样的,仔细思考就可以发现两者的不同之处:
- 数字系统(Number System
) :指数字的不同进制系统,如十进制、二进制、八进制、十六进制- 数字系统的前导
0可以省略
- 数字系统的前导
- 编码(Codes
) :较为灵活,只要求一一映射即为合法编码- 编码系统的前导
0不能省略
- 编码系统的前导
余三码补充 ¶
余三码的一个关键点在于其解决了 BCD 码的加减法进位问题,我们可以通过一个例子来明白余三码做了什么:
格雷码补充 ¶
格雷码的一种简单粗暴的写法,是通过「镜像」的技巧来倍增已知的格雷编码。
具体来说,如果现在有0 - 3的格雷码,分别是 00,01,11,10,那么我们可以将其增添一位前导 0,然后镜面对称地书写出带有前导 1 的4 - 7的格雷码。
最终我们得到的0 - 7的格雷码是:000,001,011,010,110,111,101,100
组合逻辑基础 ¶
布尔代数补充公式 ¶
香农公式(Shannon formula
基于 $X \overline{X} = 0$ 和 $X X = 1$ ,我们可以得到以下公式:
$$ x f( x, \overline{x}, y,... ) = x f( 1, 0, y,... ) $$
$$ \overline{x} f( x, \overline{x}, y,... ) = \overline{x} f( 0, 1, y,... ) $$
基于 $X + \overline{X}Y = X + Y$ 和 $X + XY = X$ ,我们可以得到以下公式(或者通过上面的公式对偶得到
$$ x + f( x, \overline{x}, y,... ) = x + f( 0, 1, y,... ) $$
$$ \overline{x} + f( x, \overline{x}, y,... ) = \overline{x} + f( 1, 0, y,... ) $$
逻辑函数分解(Shannon Expansion
$$ \begin{aligned} F(x,\overline{x},y,...) & = xf_1(x,\overline{x},y,...) + \overline{x}f_2(x,\overline{x},y,...) \cr & = xf_1(1,0,y,...) + \overline{x}f_2(0,1,y,...) \end{aligned} $$
这种分解思路可以将任何同时含有 $x$ 和 $\overline{x}$ 的函数进行分解,并转化为可以应用香农公式的形式,从而化简函数。我们可以通过给不含 $x$ 或 $\overline{x}$ 的项“与”上 $(x+\overline{x})$ 来实现该转化。
同样的,该公式也有对偶形式,这里不再赘述。
一个有趣的推论
$$ \begin{aligned} f(x,y,z) & = xyzf(1,1,1)+xy\overline{z}f(1,1,0) \cr & + x\overline{y}zf(1,0,1)+x\overline{y}\overline{z}f(1,0,0) \cr & + \overline{x}yzf(0,1,1)+\overline{x}y\overline{z}f(0,1,0) \cr & + \overline{x}\overline{y}zf(0,0,1)+\overline{x}\overline{y}\overline{z}f(0,0,0) \end{aligned} $$
标准形式与规范形式 ¶
- 标准形式提供了一种布尔表达式化简的方向(但其形式并不唯一确定,即一个表达式可以有多个标准形式)
- 规范形式提供了一种唯一确定的表达形式(这对于把复杂的逻辑运算交由机器去完成是很重要的)
SOP 与 POS:
任何表达式都可以化成 SOP 和 POS 这样的标准形式。
- SOP(Standard Sum-of-Products)即把表达式写成
OR of AND的形式; - POS(Standard Product-of-Sums)即把表达式写成
AND of OR的形式;
SOM 与 POM:
SOM(Sum of Minterms)与 POM(Product of Maxterms)蕴含着一种精巧的对称性,具体体现有:
- SOM 与 POM 的自然推导过程中,一个关键点就在于我们对
1和0谁是主体的理解,两者的推导过程是完全对称的 - SOM 与 POM 还存在一种取反的对称性,比如假设 $F(x,y,z)=\sum_m(1,3,5,7)$ ,则有 $\overline{F}(x,y,z)=\sum_m(0,2,4,6) = \prod_M(1,3,5,7)$,以及 $F(x,y,z)=\prod_M(0,2,4,6)$
任何表达式都可以化成 SOM 和 POM 这样的规范形式,以由 SOP 得到 SOM 为例:
$$ \begin{aligned} f & = x + \overline{x}\overline{y} \cr & = x(y+\overline{y}) + \overline{x}\overline{y} \cr & = xy + x\overline{y} + \overline{x}\overline{y} \end{aligned} $$
主蕴含项选择规则 ¶
主蕴含项选择规则(Prime Implicant Selection Rule)是一种卡诺图优化步骤,其主要思路是尽可能减少蕴含项的重合(overlap
- 找到所有主蕴含项;
- 选中所有「基本主蕴含项
」 ; - 选择尽量少的非基本主蕴含项来覆盖所有最小项(或最大项
) ;
Warning
请注意,基本主蕴含项也是主蕴含项,需要满足「极大」这个特征。
我们在做题的时候,往往不会按部就班地先找出所有主蕴含项,再筛选出基本主蕴含项。我们往往直接开始框选基本主蕴含项和非基本主蕴含项。有时候容易犯一些小错误,比如误会 overlap 的内涵,从而框选出了不够极大的蕴含项:
经典组合电路补充 ¶
缓冲器(Buffer
- buffer 可以作为放大器,提高电路的电压水平(回忆数字信号的宽进严出)
- buffer 可以提高电路运行的速度
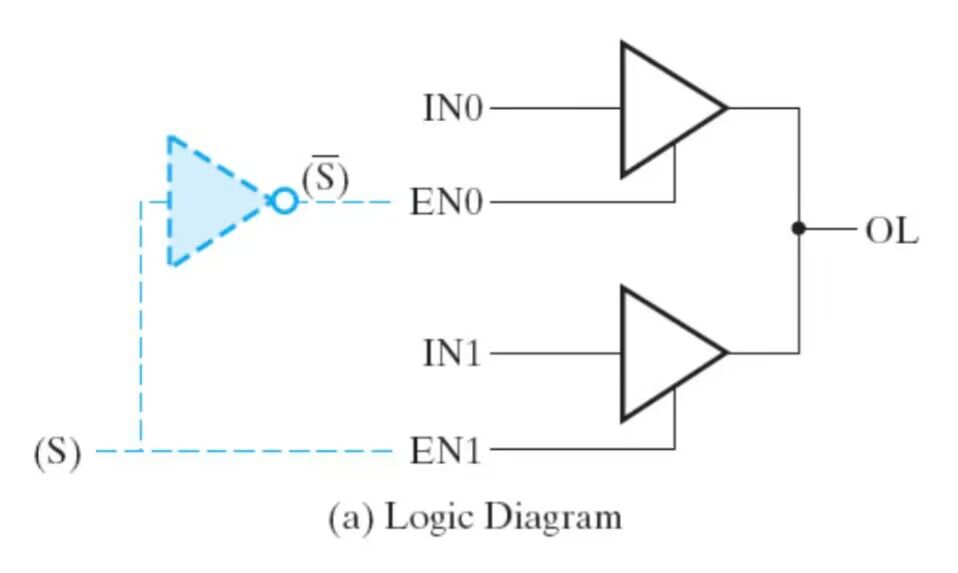
三态门(3-State Buffer)
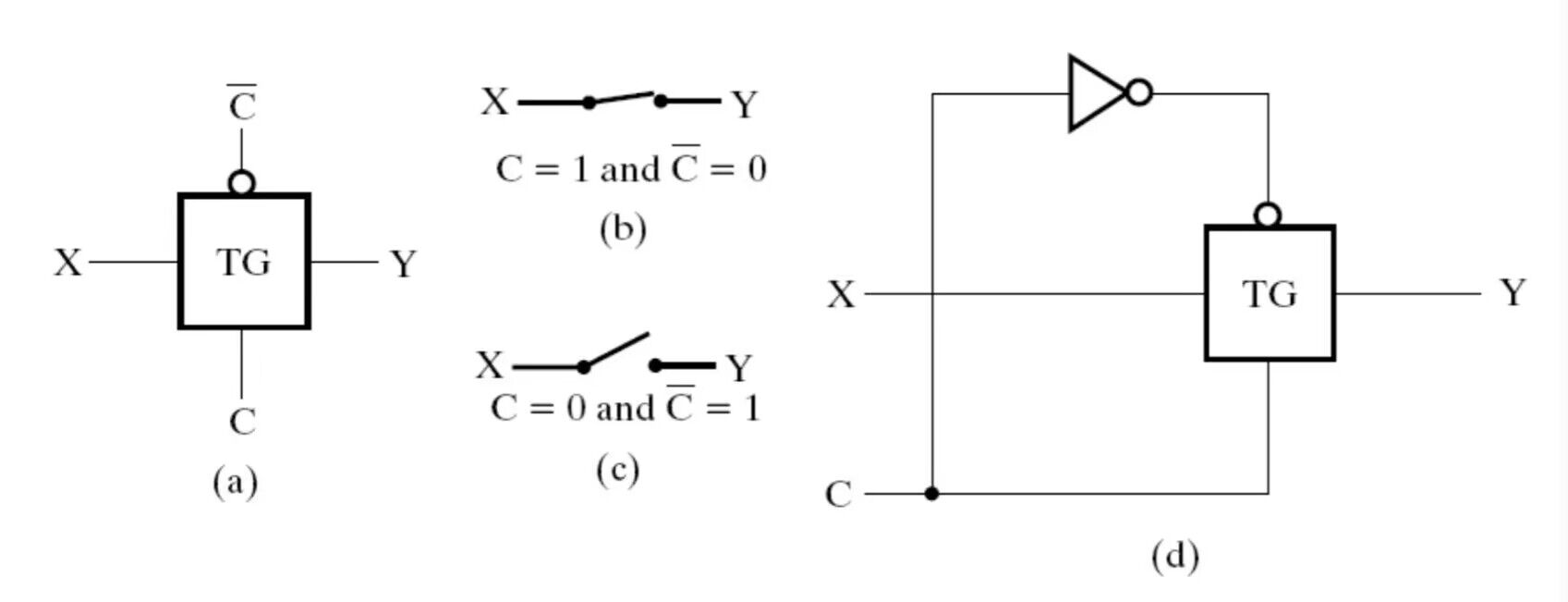
传输门(Transmission Gate)
传输门可以视为一个开关,值得注意的是:
- 传输门与三态门并不相同,尽管两者在某种意义上都可以起到开关的作用
- 关于两者具体有何区别,我暂时没有找到很合适的答案
- 传输门这个概念放在这里似乎并不合适,但是马德老师讲解到了,遂提一笔
异或门 同或门
- 异或和同或可以用来实现奇校验和偶校验。
- 而且观察其卡诺图的形状(棋盘形
) ,可以发现,它们是天然优化的,即不可优化的。
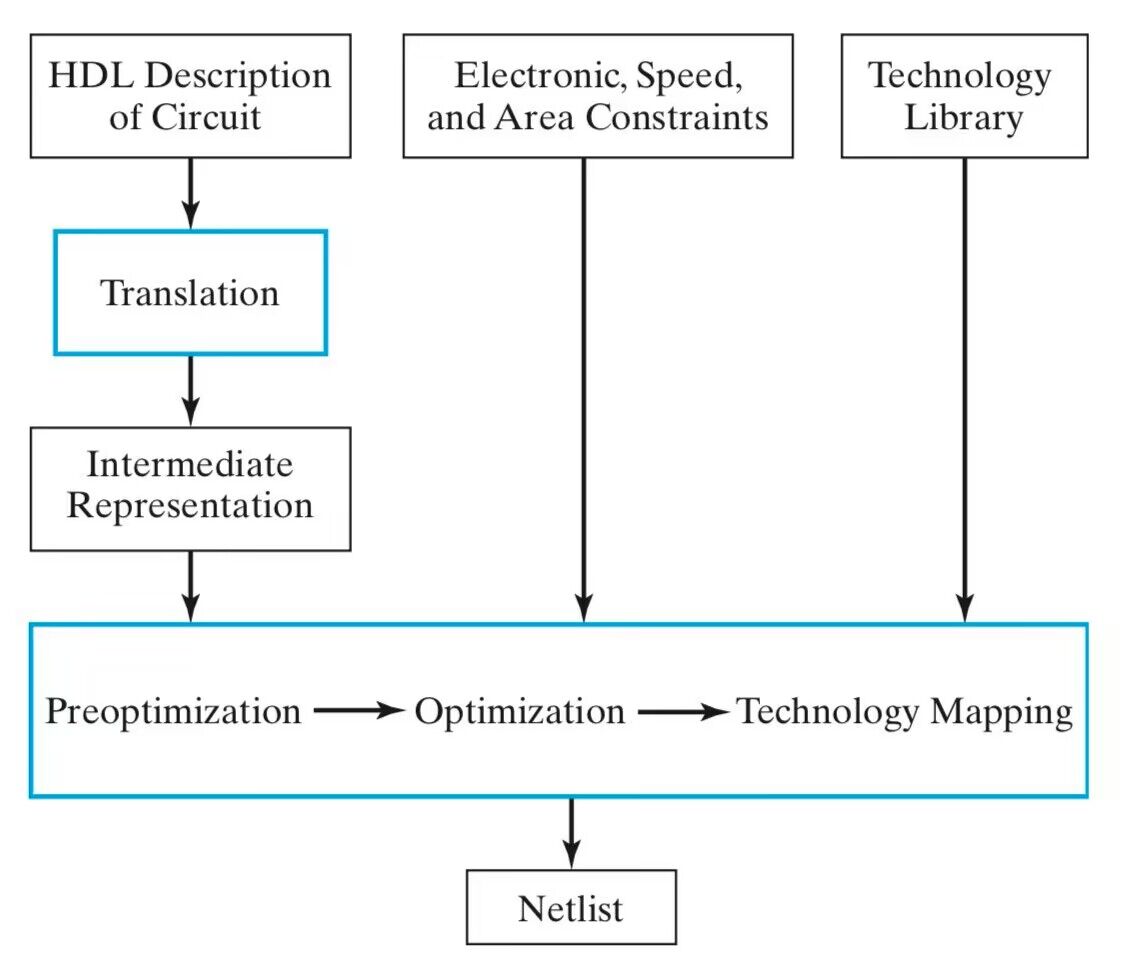
逻辑合成 ¶
逻辑合成(Logic Synthesis)是所设计数字电路的高抽象级表达,经过化简、优化后,转换到逻辑门级别的电路连线网表(netlist)的过程。
逻辑合成是电子设计自动化(EDA)中电路设计的一个步骤。
通常通过硬件描述语言(HDL)来实现电路的高级抽象。以 Verilog 为例,逻辑合成的过程可以理解为 behavioral description 转化为 structural description 的过程。
创建日期: 2024年2月8日 16:17:32