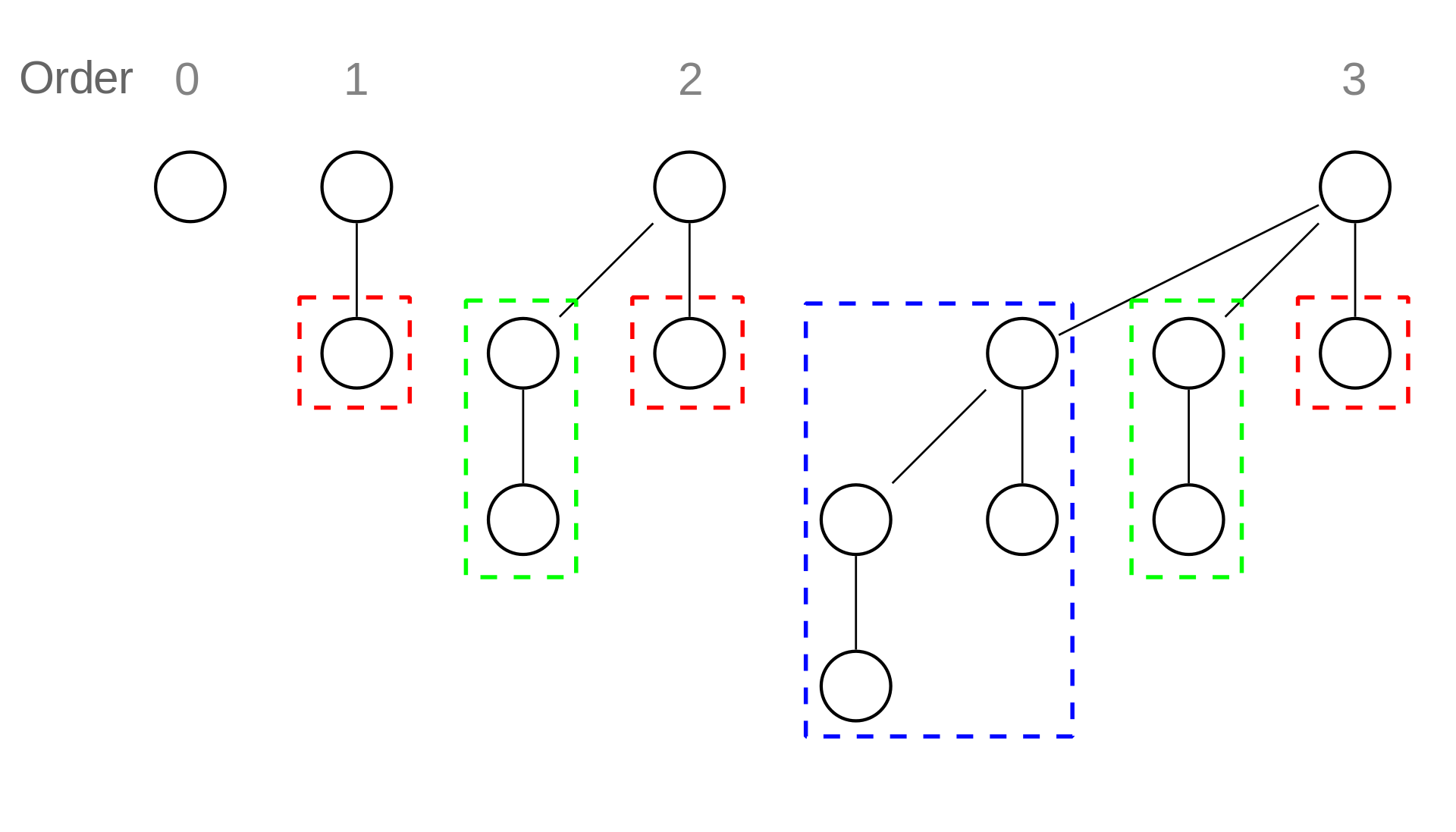高级数据结构 ¶
约 5076 个字 119 行代码 预计阅读时间 22 分钟
AVL 树 ¶
- AVL 树是一种自平衡二叉搜索树,其中每个节点的左右子树高度差不超过 1
- AVL 树的高度 $h = \Omicron(\log n)$
- AVL 树的搜索、插入和删除操作的时间复杂度均为 $\Omicron(\log n)$
再平衡 ¶
AVL 树的再平衡通过所谓的“旋转”操作实现,其精髓在于把节点在竖直方向上进行升降,而不在水平方向上做移动,从而保证二叉搜索树性质不被破坏。
旋转操作分为以下四种情况,这里记平衡因子临时为 $\pm 2$ 的节点为 X,记其较高子树的根节点为 Z,平衡因子记为 BF = 右子树高度 - 左子树高度:
- RR:Z 是 X 的右儿子,BF(Z) >= 0 => rotateLeft
- LL:Z 是 X 的左儿子,BF(Z) <= 0 => rotateRight
- RL:Z 是 X 的右儿子,BF(Z) < 0 => rotateRightLeft
- LR:Z 是 X 的左儿子,BF(Z) > 0 => rotateLeftRight
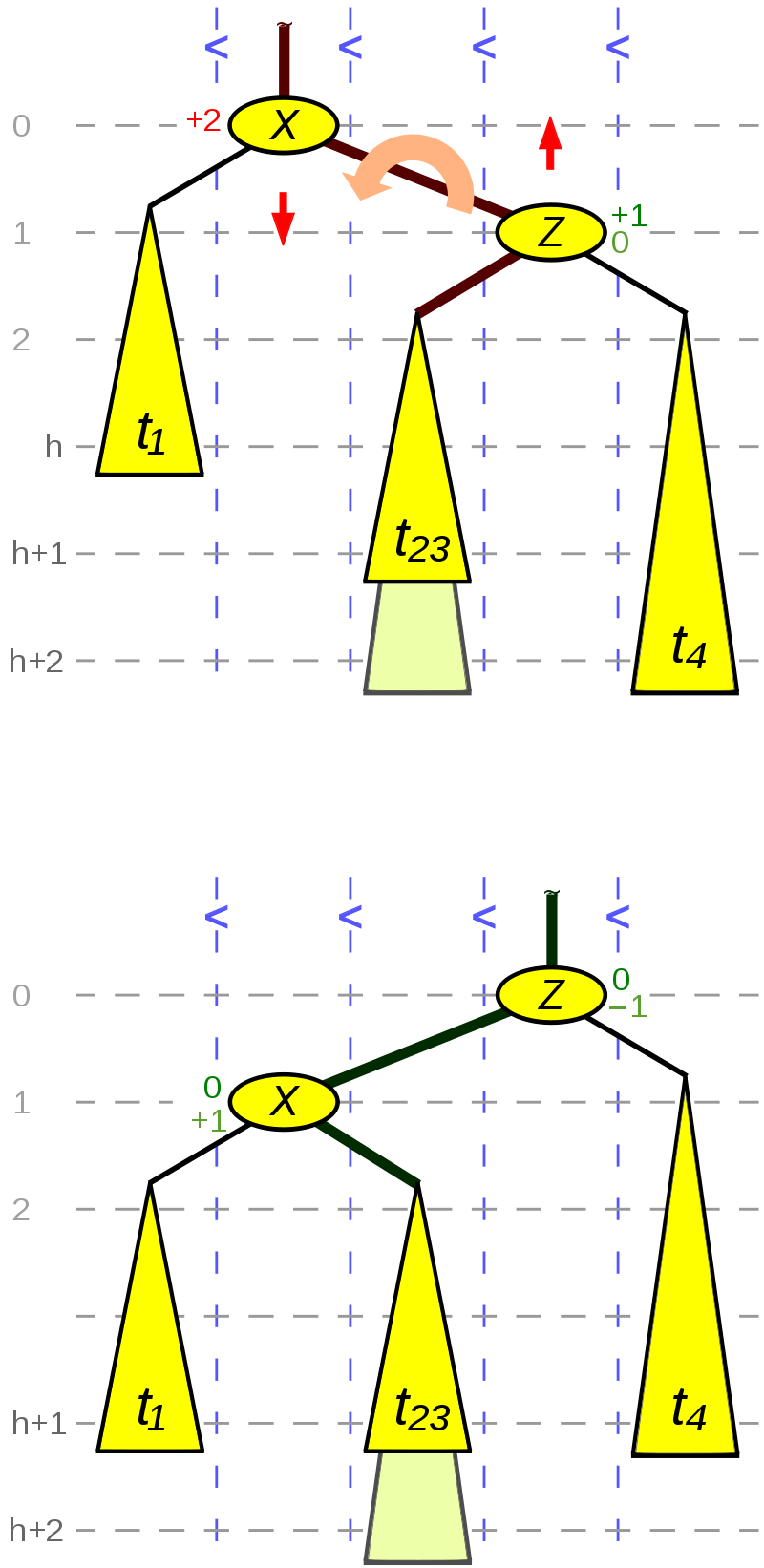
下面展示各种情况下的 rotate 操作,以 RR 和 RL 为例(LL 和 LR 对称即可
这种情况可能发生在:
- 插入操作导致 $t_4$ 高度增加 1
- 删除操作导致 $t_1$ 高度减少 1
node *rotateLeft(node *X, node *Z) {
// rotate
t23 = Z->left;
X->right = t23;
if (t23 != NULL) t23->parent = X;
Z->left = X;
X->parent = Z;
// update BF
if (BF(Z) == 0) {
// 1st case, only happens with deletion
BF(X) = +1;
BF(Z) = -1;
} else {
// 2nd case
BF(X) = 0;
BF(Z) = 0;
}
return Z; // return new root of rotated subtree
}
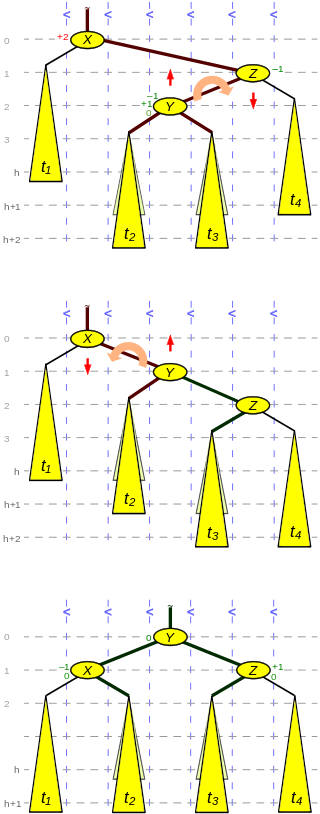
这种情况可能发生在:
- 插入 $Y$ 本身,或者插入操作导致其子树 $t_2$ 或 $t_3$ 高度增加 1
- 删除操作导致 $t_1$ 高度减少 1
node *rotateRightLeft(node *X, node *Z) {
// rotate
Y = Z->left;
t3 = Y->right;
Z->left = t3;
if (t3 != NULL) t3->parent = Z;
Y->right = Z;
Z->parent = Y;
t2 = Y->left;
X->right = t2;
if (t2 != NULL) t2->parent = X;
Y->left = X;
X->parent = Y;
// update BF
if (BF(Y) == 0) { // 1st case
BF(X) = 0;
BF(Z) = 0;
} else if (BF(Y) > 0) { // 2nd case
BF(X) = -1;
BF(Z) = 0;
} else { // 3nd case
BF(X) = 0;
BF(Z) = +1;
}
BF(Y) = 0;
return Y; // return new root of rotated subtree
}
插入与删除 ¶
AVL 树的插入和删除操作的思路都是首先进行插入和删除,然后自底向上回溯以更新 BF 值并维护平衡性,但其具体实现相当繁琐。结论是,插入后最多只需要一次 rotate 即可实现再平衡,而删除后可能需要多次 rotate 才能实现再平衡(最坏情况需要 $\log n$ 次
- 用二叉搜索树的插入操作插入新节点
- 从新插入的节点开始向上回溯,并不断更新节点的 BF 值:
- 如果 BF: $\pm 1$ -> 0,停止回溯
- 如果 BF: 0 -> $\pm 1$,继续回溯
- 如果 BF: $\pm 1$ -> $\pm 2$,执行相应的 rotate 操作,并停止回溯(原因:注意到这时候 rotate 返回的子树具有与插入前相同的高度,且其根节点 BF = 0)
具体代码实现可以参考这里。
- 用二叉搜索树的删除操作删除目标节点
- 从被删除的节点开始向上回溯,并不断更新节点的 BF 值:
- 如果 BF: 0 -> $\pm 1$,停止回溯
- 如果 BF: $\pm 1$ -> 0,继续回溯
- 如果 BF: $\pm 1$ -> $\pm 2$,执行相应的 rotate 操作,并视情况判断是否需要继续回溯(若 rotate 返回的子树具有与删除前相同的高度,则停止回溯;若 rotate 返回的子树高度比删除前小 1,则继续回溯)
具体代码实现可以参考这里。
Splay 树 ¶
- Splay 树通过将所有访问操作与所谓“展开”操作相结合,从而实现均摊对数时间复杂度
- Splay 树使得最近访问的节点被移动到根节点附近,从而可以快速再次访问,具有较好的访问局部性
- Splay 树不具备严格的自平衡能力,最坏情况下高度可能是线性的(例如以非降序访问所有节点后就会出现这种情况)
- Splay 树的搜索、插入和删除操作的摊还时间复杂度均为 $\Omicron(\log n)$
展开 ¶
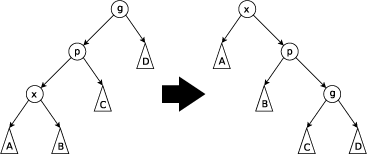
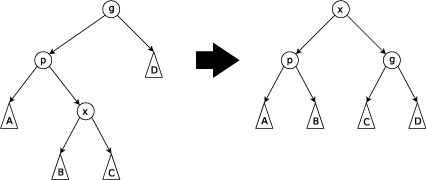
展开操作分为以下三种情况,这里记待移动到根节点的节点为 X,记其父节点为 P,如果父节点的父节点存在,则记为 G;素材源自 Wikipedia:
当 G 存在且 X 和 P 都是左儿子或右儿子时执行此步骤。
具体来说是首先对 P 和 G 进行 rotate,然后再对 X 和 P 进行 rotate;注意这里的顺序是重要的,如果反过来操作的话,则是一种由 Allen & Munro 提出的 naive 的实现方式,会导致无法实现均摊对数时间复杂度。
所有的访问操作(搜索、插入和删除)都会引发展开操作:
- 搜索:直接找到目标节点并对其进行展开即可
- 插入:用二叉搜索树的插入操作插入新节点,并对其进行展开
- 删除:用二叉搜索树的删除操作删除目标节点,并对其父节点进行展开
- 或者,将目标节点展开到树的根节点位置,然后删除根节点并合并左右子树
摊还分析 ¶
摊还分析(amortized analysis)从空的结构开始,考虑可能出现的操作序列中的最差序列。
摊还分析是一种有用的工具,可以补充最差情况和平均情况分析:一方面摊还分析排除不可能出现的操作序列,因而不像简单粗暴的最差情况分析那么悲观;另一方面摊还分析比平均情况分析更加容易,毕竟后者涉及“如何定义平均情况”等概率问题。
摊还分析常见方法有以下三种:
- 聚合法:寻找可能出现的操作序列中的最差序列并分析其成本 $T(n)$,直接用 $T(n)/n$ 表示每个操作的摊还成本
- 核算法:使用“截长补短”思想,为每一种操作估计摊还成本 $\hat{c _ i} = c _ i + \varDelta _ i$ 且 $\sum _ {i=1} ^ n \hat{c _ i} \geq \sum _ {i=1} ^ n c _ i$
- 势能法:使用“截长补短”思想,设计势能函数 $\varPhi (D _ i)$,为每一步操作估计摊还成本 $\hat{c _ i} = c _ i + (\varPhi (D _ i) - \varPhi (D _ {i-1}))$ 且 $\varPhi (D _ n) \geq \varPhi (D _ 0)$
- Splay 树的势能法摊还分析可以参考修佬的笔记
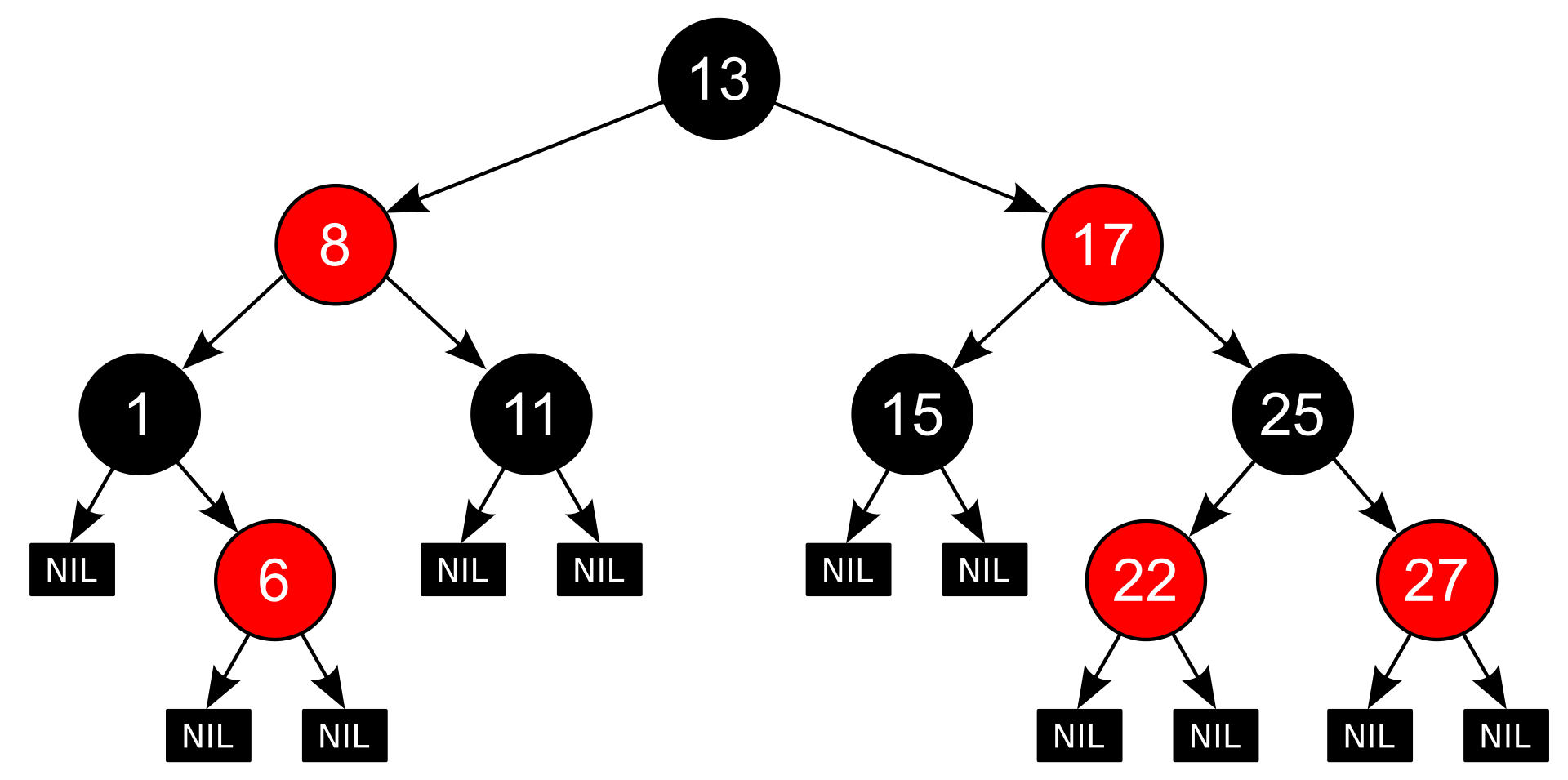
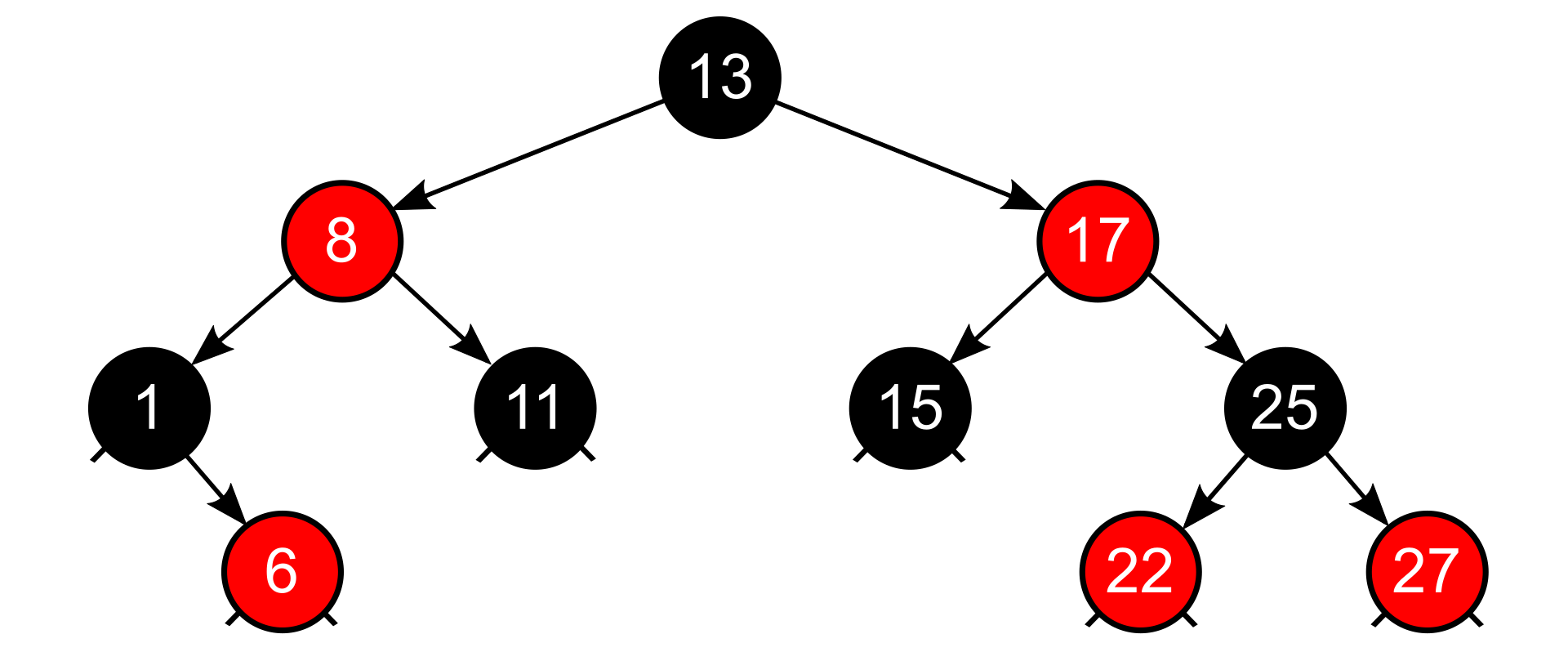
红黑树 ¶
- 红黑树是满足如下五条性质的二叉搜索树:
- 每个节点或者是红色的,或者是黑色的;
- 根节点是黑色的(optional)
- 叶节点(NIL)是黑色的;
- 红色节点的子节点都是黑色的;
- 对于每个节点,从该节点到其所有后代 NIL 的简单路径上,包含的黑色节点个数(称为该节点的黑高)相同
- 红黑树的高度至多为 $2\log (n+1)$,其中 $n$ 为节点总数(不含 NIL)
- 红黑树的搜索、插入和删除操作的时间复杂度均为 $\Omicron(\log n)$
插入 ¶
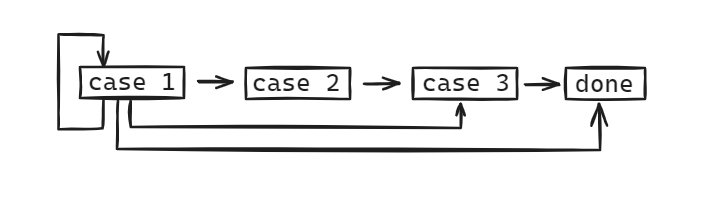
为了尽量不破坏平衡性质,每次插入的新节点默认染成红色。如果新节点插入空树则只需染黑即可,如果新节点插入在黑色节点下面则无需调整,而如果新节点插入在红色节点下面则有可能破坏平衡,具体可以分为以下三种情况:
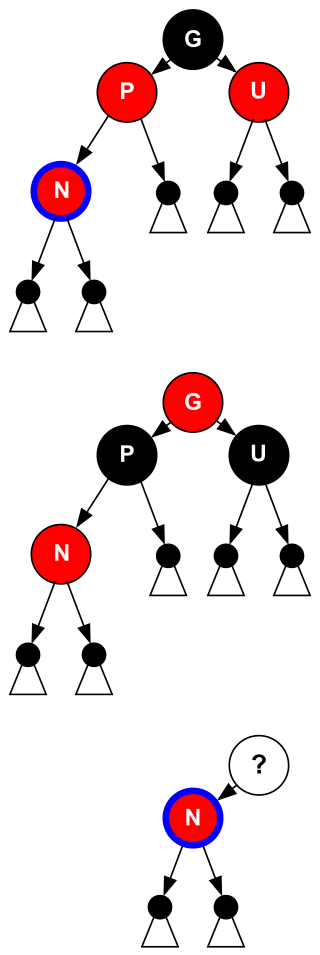
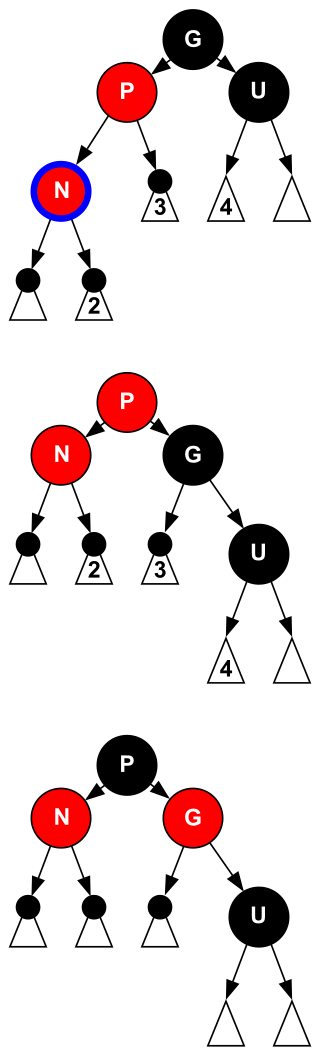
以新节点 N 插入在祖父 G 左侧为例(右侧对称即可
- case 1:N 的叔叔 U 是红色的,无论 N 是左儿子还是右儿子
- 将父亲 P 和叔叔 U 染黑,并把祖父 G 染红
- 此时祖父 G 有可能引发新的问题(如果 G 的父亲是红色的)并向上递归做调整
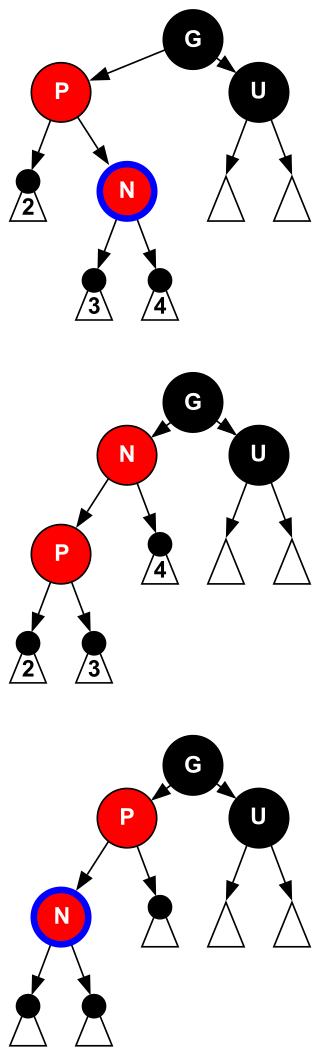
- case 2:N 的叔叔 U 是黑色的,且 N 是右儿子
- 对 N 和父亲 P 进行 rotate,与 AVL 树的 rotateLeft 操作是一致的
- 此时问题还没有解决,但是转变为 case 3
- case 3:N 的叔叔 U 是黑色的,且 N 是左儿子
- 对 P 和祖父 G 进行 rotate,与 AVL 树的 rotateRight 操作是一致的
- rotate 操作后交换 P 和 G 的颜色(事实上所有的 rotate 操作都伴随着颜色互换)
删除 ¶
回顾二叉搜索树的删除操作不难发现,第三种情况可以通过一步交换(注意这里只交换键值不交换颜色)直接转化为第一或第二种情况,因此我们只需要关注第一和第二种情况。第一种情况中替代被删除节点的是 NIL,第二种情况替代被删除节点的是其子节点。如果被删除的节点是红色的则无需调整,如果被删除的节点是黑色的且替代上来的节点是红色则只需染黑即可。
而如果被删除的节点是黑色的且替代上来的节点也是黑色的(注意 NIL 也是黑色的
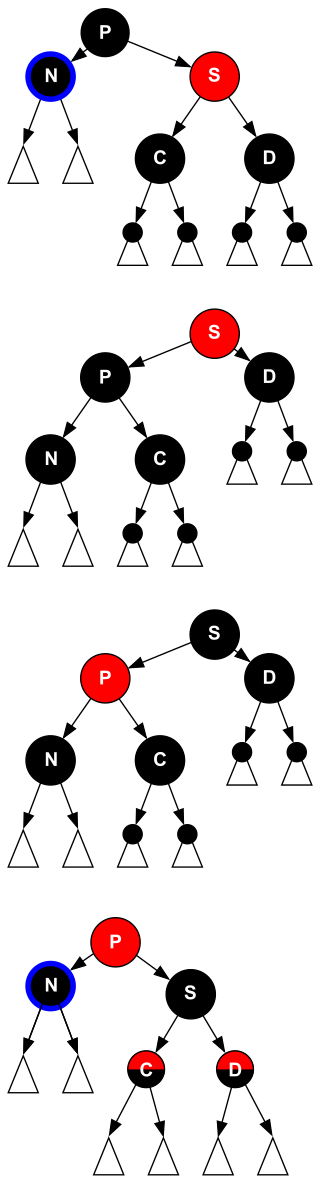
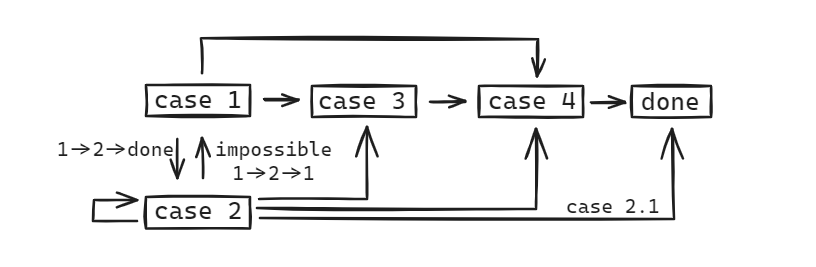
以被删除的节点 N 位于父亲 P 左侧为例(右侧对称即可
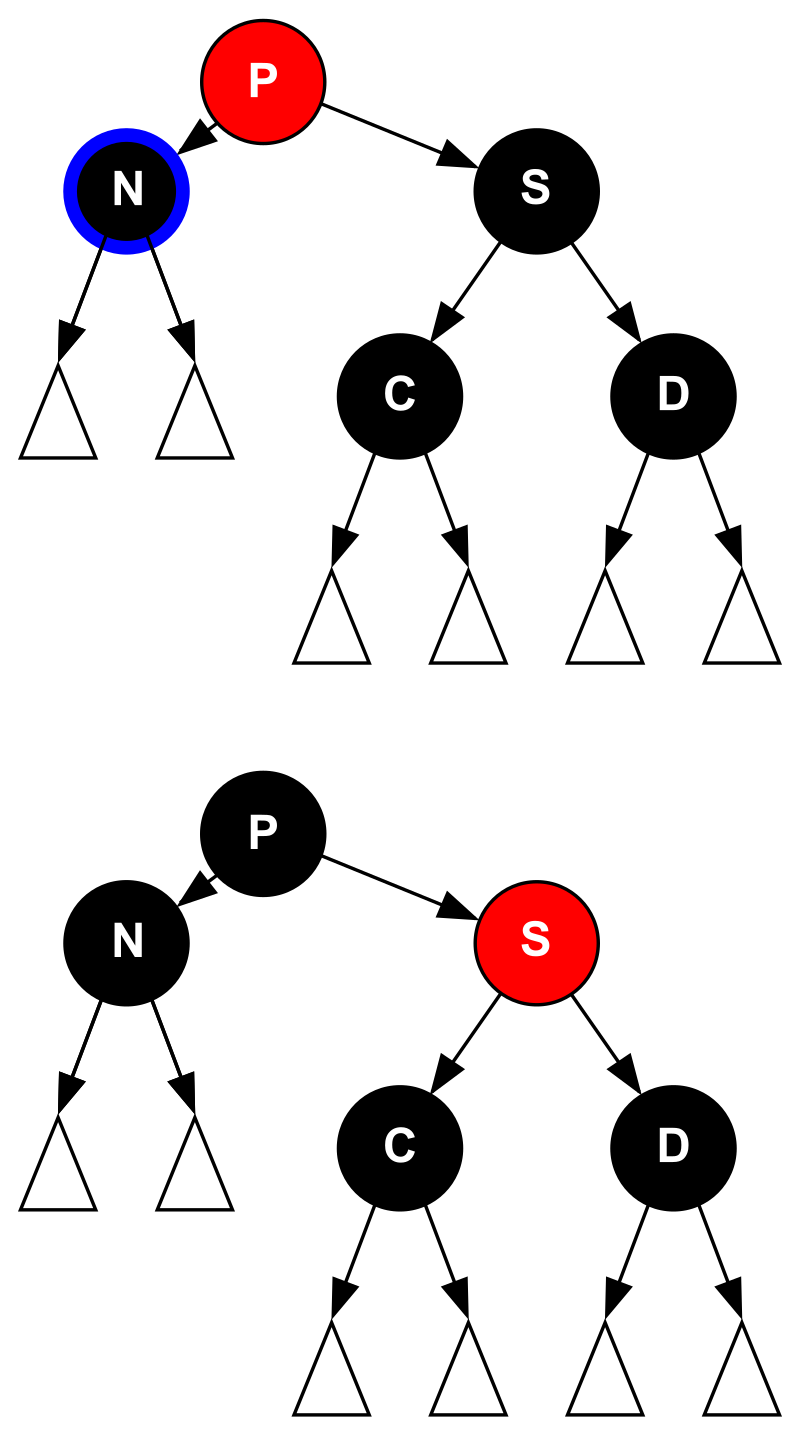
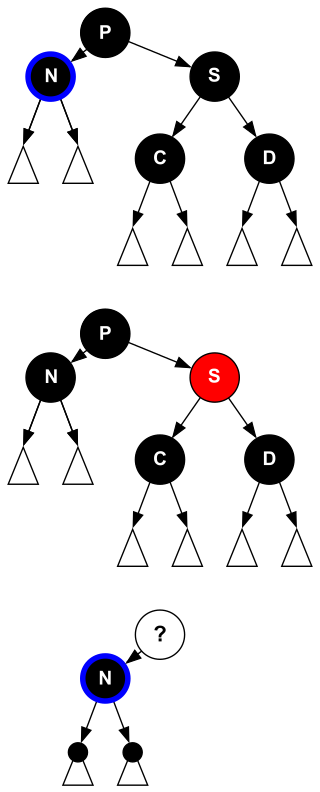
- case 1:N 的兄弟 S 是红色的
- 对 S 和父亲 P 进行 rotate,与 AVL 树的 rotateLeft 操作是一致的;并交换颜色
- 此时“双黑”还没有被解决,转变为其他 case
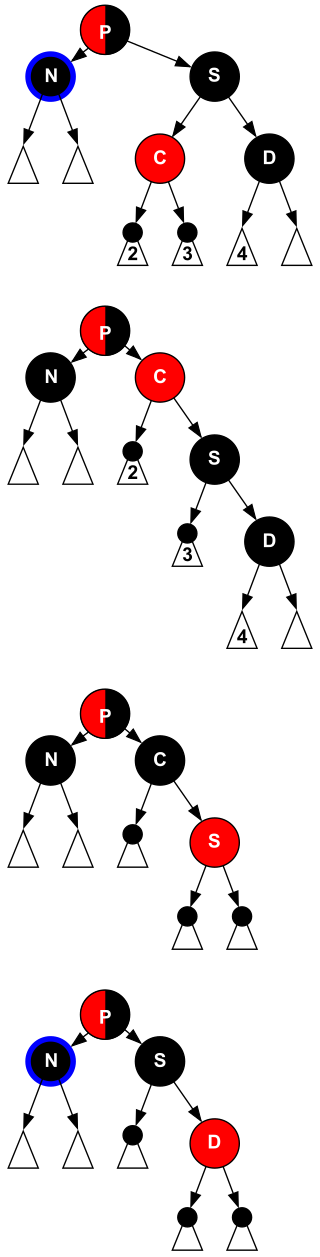
- case 2:N 的兄弟 S 是黑色的,且 S 的两个儿子也都是黑色的
- 问题可以根据 P 的颜色进一步细分成 2.1 和 2.2
- 2.1 首先将 S 染红并将 N 去掉一重黑色,然后将 P 染黑,问题解决
- 2.2 首先将 S 染红并将 N 去掉一重黑色,然后将 P 染成“双黑”,问题向上递归
- case 3:N 的兄弟 S 是黑色的,且近侄子 C 是红色的,远侄子 D 是黑色的
- 对 C 和 S 进行 rotate,与 AVL 树的 rotateRight 操作是一致的;并交换颜色
- 此时“双黑”还没有被解决,转变为 case 4
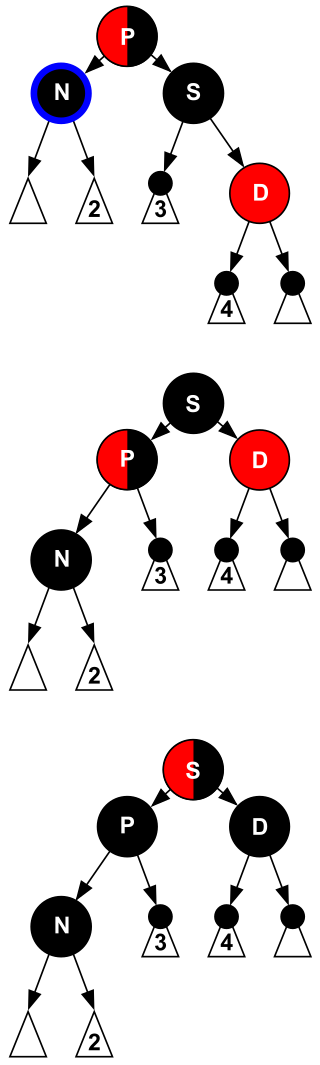
- case 4:N 的兄弟 S 是黑色的,且远侄子 D 是红色的,近侄子随意
- 对 S 和 P 进行 rotate,与 AVL 树的 rotateLeft 操作是一致的;并交换颜色
- 然后将 D 染黑并将 N 去掉一重黑色,问题解决
比较 AVL 树与红黑树 ¶
- 总的来说 AVL 树是严格平衡的,而红黑树只是严格的黑高平衡,其中红色节点是少量不平衡的因素;除此之外,两者都是通过旋转实现再平衡,没有很大的差别;但有趣的是,很多库函数在选择平衡搜索树实现功能时会更常用红黑树(例如 C++ 的 std::map 和 Java 的 HashMap 等)
- AVL 树最差高度约为 $1.44 \log n$,红黑树最差高度约为 $2 \log n$,从而如果对一棵树的搜索操作居多,则 AVL 树可能会是更好的选择
- AVL 树虽然插入只需要常数次旋转,但在删除时可能需要 $\Omicron(\log n)$ 次旋转,而红黑树的插入和删除都最多只需要常数次旋转;很多人认为代码实现时旋转是插入和删除中开销最大的操作,从而如果对一棵树的插入和删除操作很多,AVL 树不如红黑树快
- AVL 树需要维护平衡因子,而红黑树只需要 1 bit 来表示红与黑,更节省空间
- 红黑树是可持久化的数据结构,因此在函数式编程中容易实现;而且红黑树支持分裂、合并等操作,这使得它可以做批量并行的插入、删除
B+ 树 ¶
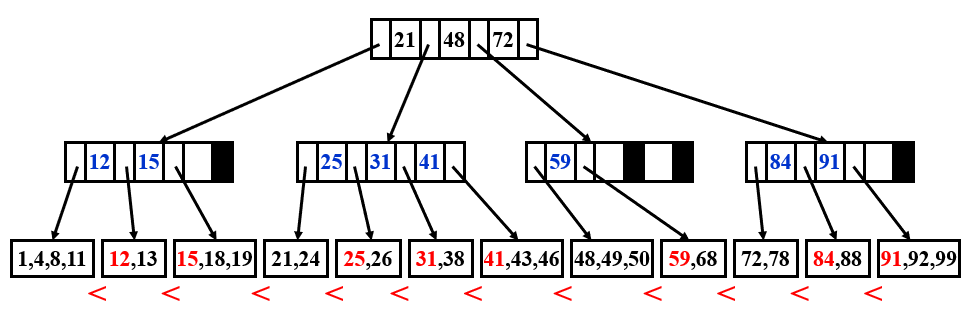
- $M$ 阶 B+ 树是满足如下性质的树:
- 根节点或者是叶子,或者有 2 到 $M$ 个儿子
- 非叶节点(根节点除外)索引 $\lceil M/2 \rceil$ 到 $M$ 个儿子
- 叶子节点(根节点除外)存储 $\lceil M/2 \rceil$ 到 $M$ 个数据
- 2-3-4 树(4 阶)和 2-3 树(3 阶)这种别称表达了节点可能含有的儿子个数
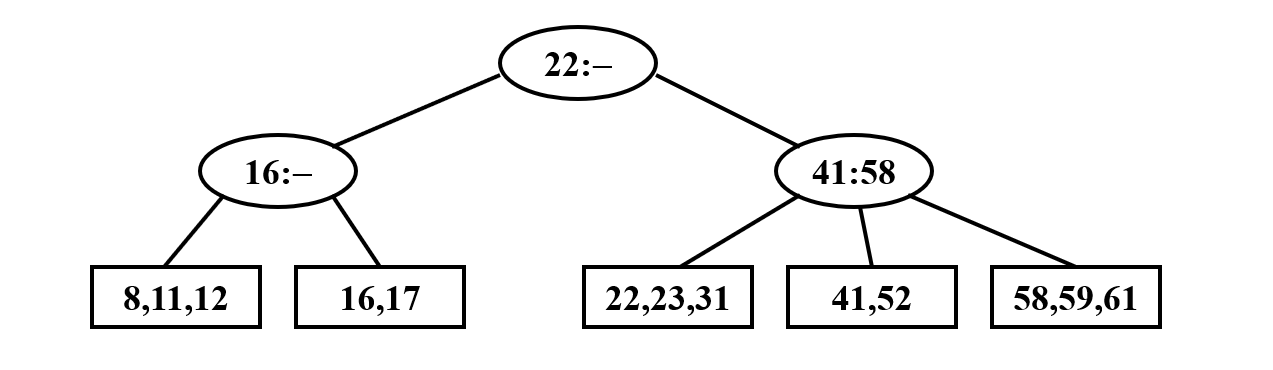
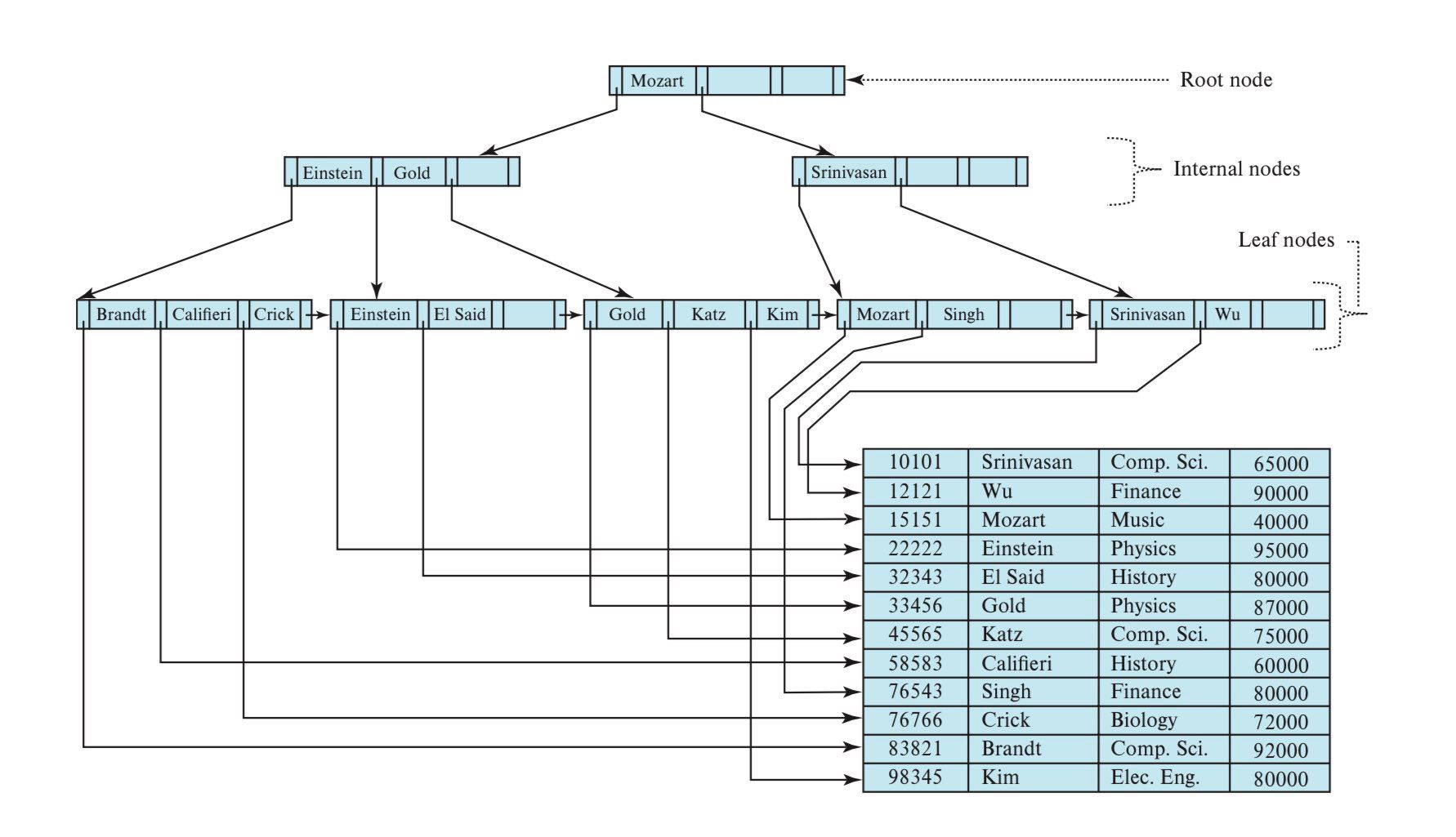
- 不同地方对 B+ 树的定义并不完全相同,这里给出一些版本(前两张来自这门课程的 PPT,第三章来自数据库教材 Database System Concepts 7 th)
搜索、插入与删除 ¶
- 搜索:搜索方法是很显然的
- 一方面,树的高度不超过 $\Omicron(\log _ {\lceil M/2 \rceil} N)$;另一方面,由于每层的键值是有序的,可以通过二分查找判断搜索方向,复杂度为 $\Omicron(\log _ 2 M)$;综上可得搜索的时间复杂度为 $\Omicron(\log _ {\lceil M/2 \rceil} N \cdot \log _ 2 M) = \Omicron(\log N)$
- 插入:插入方法也是很显然的,当节点溢出时,分裂节点并向上传递
- 一方面,树的高度不超过 $\Omicron(\log _ {\lceil M/2 \rceil} N)$;另一方面,每层的操作最多是 $\Omicron(M)$ 的;综上可得插入的时间复杂度为 $\Omicron(\log _ {\lceil M/2 \rceil} N \cdot M) = \Omicron(\frac{M}{\log M} \log N)$
- 删除:当节点向下溢出时,尝试重新分配键值(与相邻的兄弟节点)或直接合并节点(当重新分配失败时)
- 删除的时间复杂度分析与插入类似,也为 $\Omicron(\frac{M}{\log M} \log N)$
平衡二叉搜索树与 B+ 树 ¶
- B+ 树和 AVL 树、红黑树等平衡二叉搜索树的目的不完全一致:前者服务于数据库系统或文件系统,搜索存储在硬盘中的海量数据,而后者服务于一般的内存运算
- B+ 树具有极小的树高($M$ 很大时)从而磁盘寻路次数大幅减少,适合于以页为单位读写的存储系统
- 事实上红黑树的提出正是为了更方便的实现 B 树,我们学习的红黑树对应于 2-3-4 树,而 Sedgewick 提出的一种变体左倾红黑树则对应于 2-3 树
倒排索引 ¶
- 倒排索引是一种数据库索引,存储从内容到其在文档中位置的映射
- 倒排索引的目的是支持快速全文搜索,代价是将新文档添加进数据库时开销较大
倒排索引相关内容比较简单,这里仅列出一些值得注意的细节:
- 倒排索引中保存单词的出现频次是因为当搜索包含多个关键字时,从频次较少的词开始搜索会更快
- 倒排索引的构建有很多技巧,比如 stemming、stop words 等分词策略,访问单词时选择使用搜索树还是哈希,分布式外存选择 term-partitioned 还是 document-partitioned
- 搜索引擎的评价:
- 区分 data retrieval 和 information retrieval,前者搜索的是结构化的数据,后者搜索的是非结构化的文章、网页等
- 响应时间和索引空间都是评价这两种搜索的指标,而答案集的相关度则只针对后者
- 答案集的相关度可以通过准确度、回调率等指标量化
左式堆 ¶
经典的二叉堆可以在 $\Omicron(\log n)$ 时间内实现插入、删除、修改权值等操作,以及线性时间建堆。而对于合并操作,最好的方法似乎是直接合并两个存储二叉堆的数组并建堆,时间复杂度为 $\Omicron(n)$,而我们希望合并操作也能在 $\Omicron(\log n)$ 时间内完成,所以需要定义新的数据结构,也就是下文的三种可合并堆。
- 节点的零路径长 Npl 定义为从该节点到一个没有儿子的节点的最短路径长度,且规定 Npl(null) = -1
- Npl(X) = min{ Npl(X->left), Npl(X->right) } + 1
- 左式堆要求每个节点的左儿子 Npl 大于等于右儿子 Npl
- 左式堆中若右路径上有 $r$ 个节点,则整个堆至少有 $2 ^ r - 1$ 个节点
合并 ¶
左式堆的插入、删除最小值(或最大值)都最终归结于合并操作,时间复杂度也完全来源于合并操作:
- 插入可以视作一个左式堆和一个单节点的左式堆的合并
- 删除最小值(或最大值)直接删除根节点并合并两个子树即可
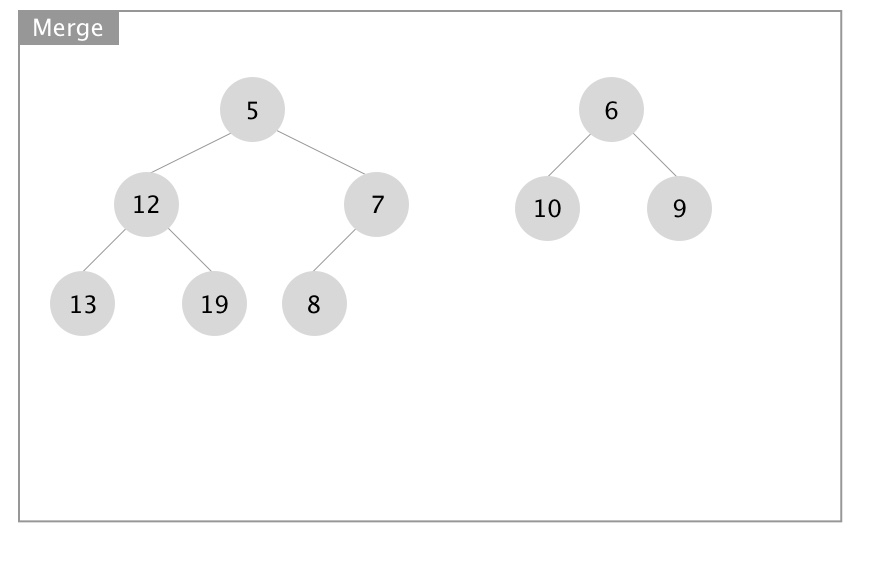
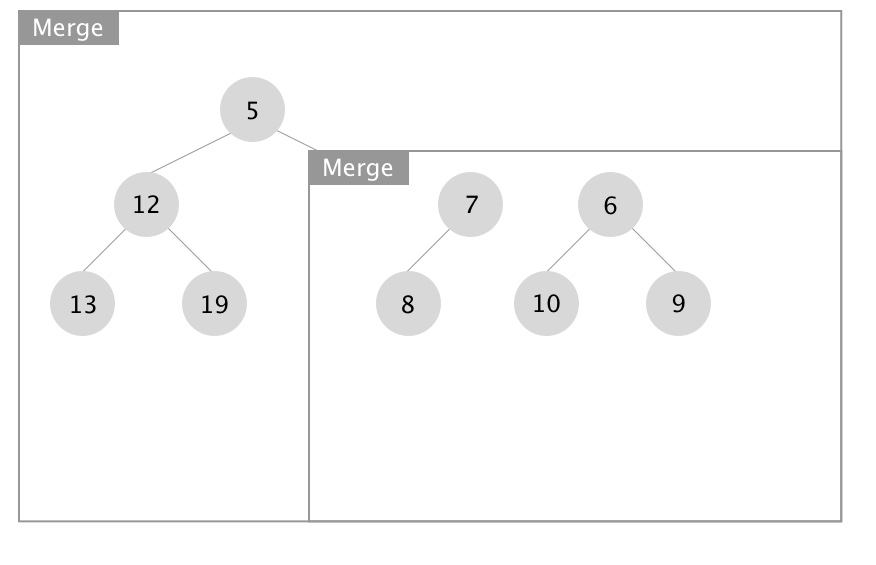
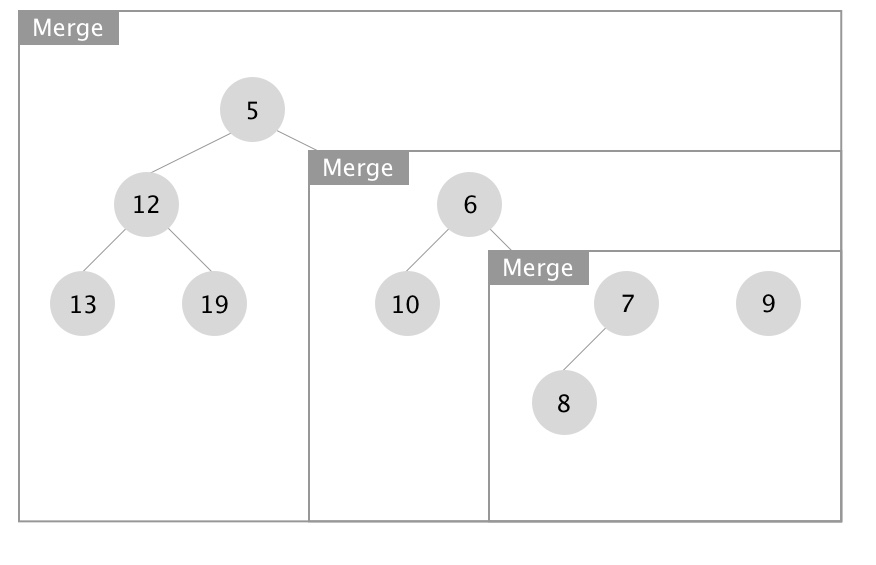
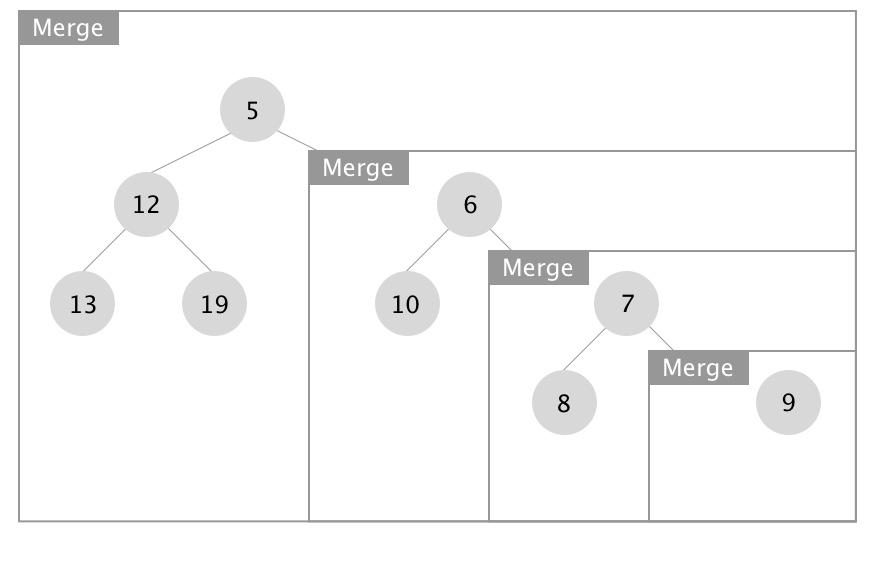
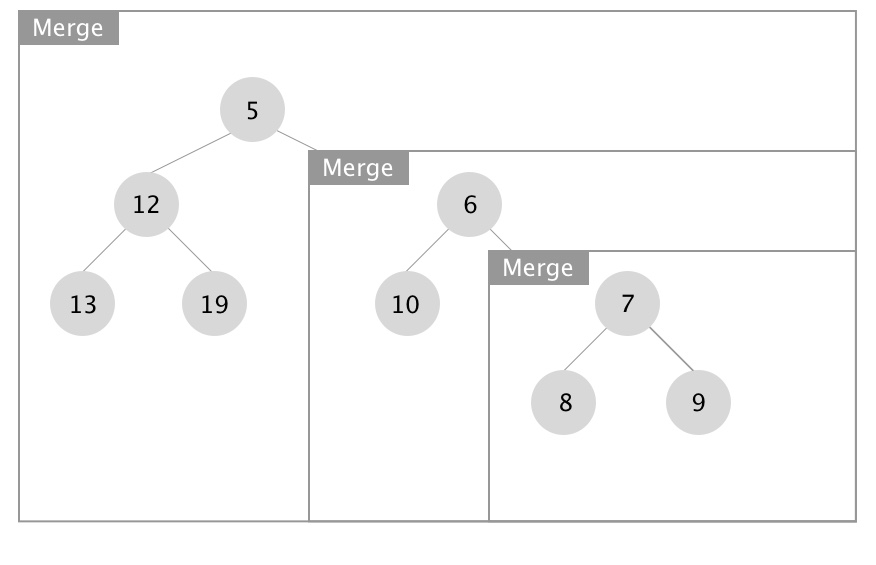
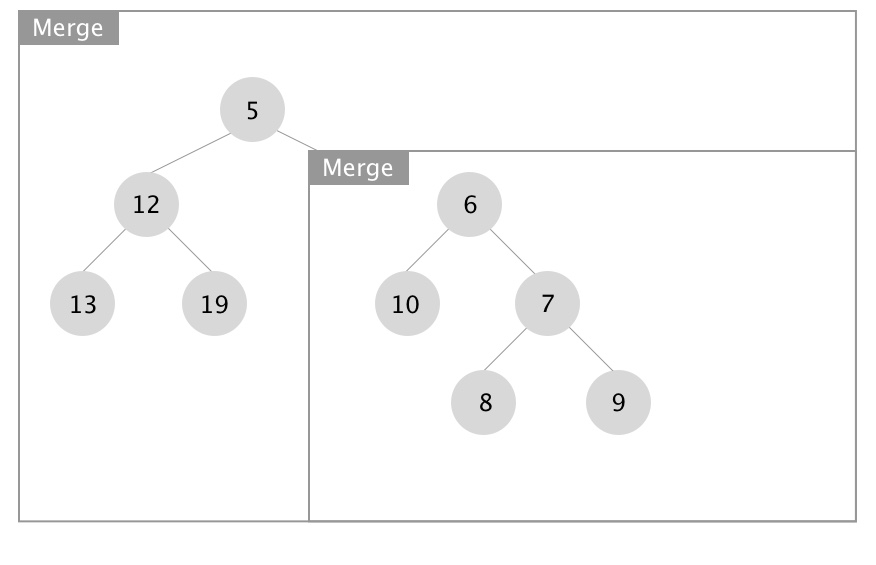
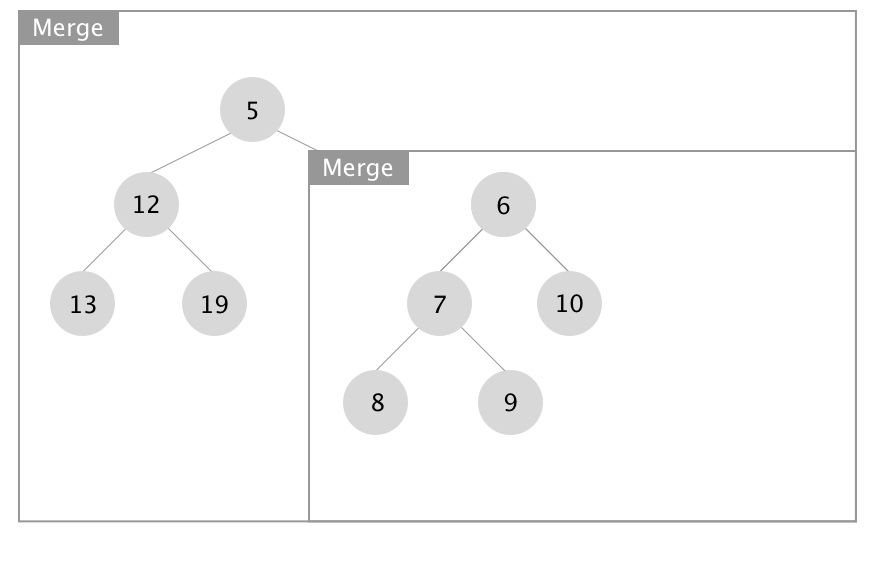
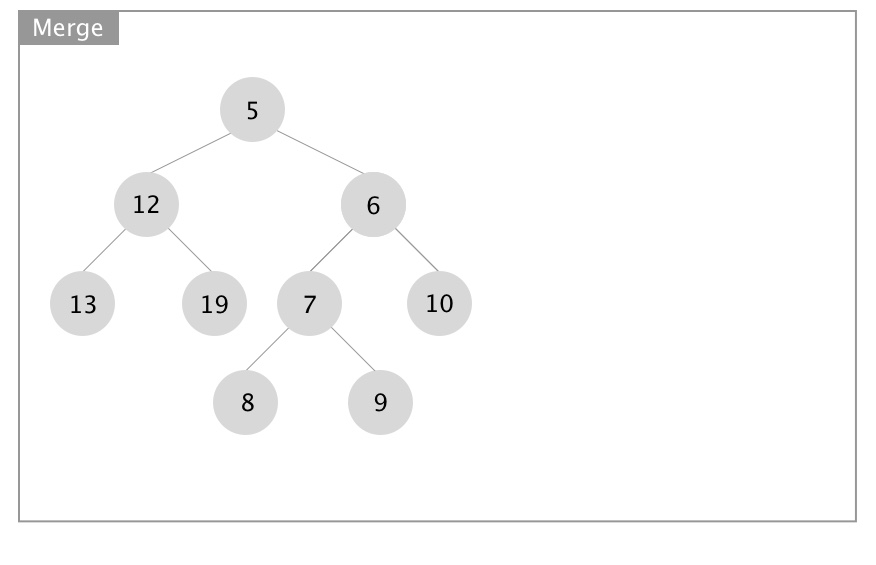
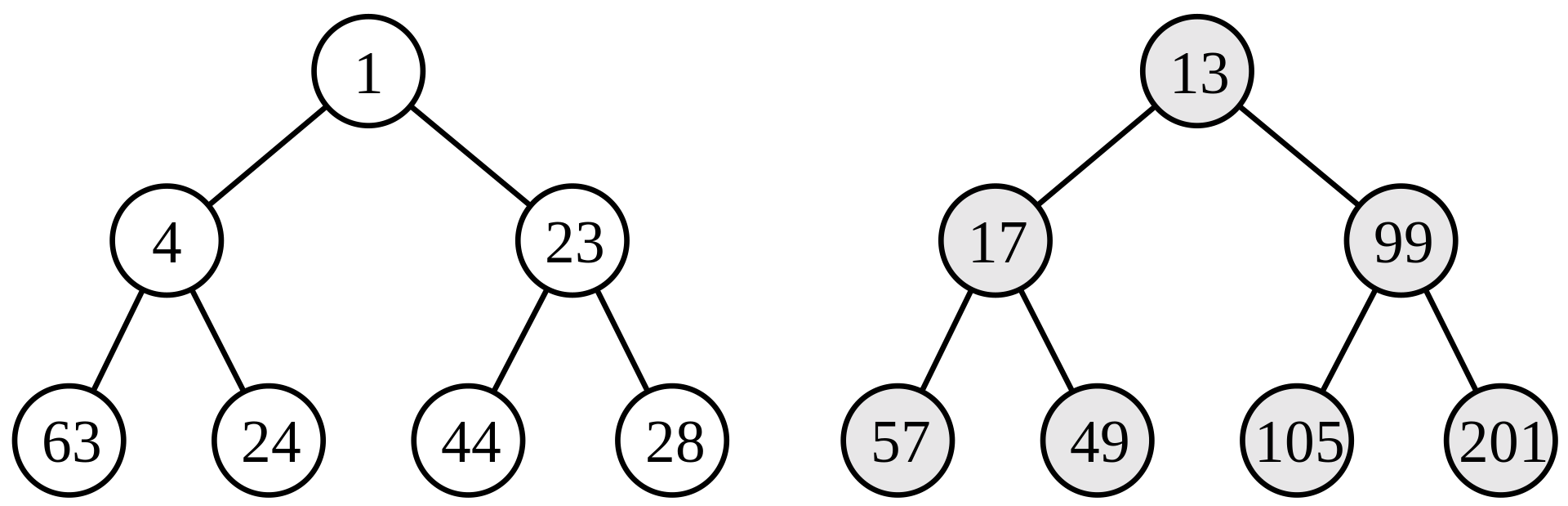
下面展示合并操作的递归实现,图片源自 Wikipedia:
- 向下递进进行堆的合并
- 向上回归进行 Npl 的更新
PriorityQueue merge(PriorityQueue H1, PriorityQueue H2) {
if (H1 == NULL) return H2;
if (H2 == NULL) return H1;
if (H1->Element < H2->Element) return mergeHelper(H1, H2);
else return mergeHelper(H2, H1);
}
static PriorityQueue mergeHelper(PriorityQueue H1, PriorityQueue H2) {
if (H1->Left == NULL) {
H1->Left = H2;
} else {
H1->Right = merge(H1->Right, H2);
if (H1->Left->Npl < H1->Right->Npl)
swapChildren(H1);
H1->Npl = H1->Right->Npl + 1;
}
return H1;
}
合并操作的时间复杂度为 $\Omicron(\log n _ 1 + n _ 2) = \Omicron(\log n _ 1 n _ 2) = \Omicron(\log \sqrt{n _ 1 n _ 2}) = \Omicron(\log (n _ 1 + n _ 2))$,其中 $n _ 1, n _ 2$ 分别表示两个堆的节点数,注意到最后一步运用了基本不等式。
左式堆的合并操作也可以通过迭代实现,具体可以理解为首先进行一个排序并合并(排序的对象是两个堆右路径上的各个节点及其左子树
斜堆 ¶
- 斜堆与左式堆的关系类似于 Splay 树与 AVL 树的关系
- Splay 树不再维护 BF,而是在每次访问节点后不断将其向上翻直至根节点
- 斜堆不再维护 Npl,而是在合并过程中不断将左右子树做交换直至合并完成
- 斜堆的合并操作的摊还时间复杂度为 $\Omicron(\log n)$,其中 $n = n _ 1 + n _ 2$
合并 ¶
最直观的理解类似于左式堆的迭代式合并,将两个原始堆的右路径节点排序后依次放在堆的左路径上,且它们的左子树都换到各自的右边。
摊还分析 ¶
摊不动一点……
二项堆 ¶
经典的二叉堆可以在 $\Omicron(n)$ 时间内实现 $n$ 个节点的插入建堆操作,从而拥有常数的均摊时间,而左式堆和斜堆不可以。二项堆的引入是为了在保持对数时间合并操作的条件下进一步优化插入的时间复杂度。
- 二项堆是由若干二项树(阶数相异且满足堆性质)构成的森林
- $k$ 阶二项树有 $2 ^ k$ 个节点,深度为 $d$ 的节点数是二项系数 $\begin{pmatrix} k \cr d \end{pmatrix}$
- 二项堆的结构与二进制是相呼应的,可以借助二进制帮助理解
- 二项堆的插入操作是 $\Omicron(\log n)$ 的,但从空开始建堆的时间复杂度是 $\Omicron(1)$ 的
合并、插入与删除 ¶
插入与删除最小值操作都可以归结于合并操作:插入相当于合并一个单节点的 $0$ 阶二项树;删除最小值操作首先用 $\Omicron(\log n)$ 时间找到最小值,然后合并两个堆,其一是原始堆移除 $B _ k$ 后剩下的堆,其二是 $B _ k$ 移除根节点后剩下的堆。
摊还分析 ¶
求解从空开始插入建堆的时间复杂度可以进行摊还分析。
最简单的一种思路是聚合法,类比合并操作与二进制加法可以发现,从空开始插入 $n$ 个节点建堆的时间复杂度与从 $0$ 开始不断加 $1$ 做二进制加法时比特翻转总次数是一致的。具体而言,最低位每次加 $1$ 都会翻转,次低位每两次加 $1$ 翻转一次,倒数第三位每四次加 $1$ 翻转一次……以此类推 $n$ 次操作的时间复杂度为 $\Omicron(n + \frac{n}{2} + \frac{n}{4} + \cdots + \frac{n}{2 ^ {\lfloor \log n \rfloor + 1}}) = \Omicron(2n)$,从而单步操作的摊还时间是 $\Omicron(1)$ 的。
创建日期: 2024年3月12日 20:05:28